题目内容
18．
如图所示，在△ABC中，I为△ABC的内心，AI交BC于D，交△ABC外接圆于E求证：
（1）IE=EC
（2）IE2=ED•EA．
分析 （1）利用三角形内心与角平分线的性质、圆的性质即可得出．
（2）利用△ECD∽△EAC即可证明．
解答 证明：（1）连接IC，QI为内心，
∴∠3=∠4，∠1=∠2．
∴∠1=∠5，∴∠5=∠2．
∴∠3+∠2=∠4+∠5．
∴∠EIC=∠ECI，
∴IE=CE．
（2）∵∠E=∠E，∠5=∠2．
∴△ECD∽△EAC，
∴$\frac{CE}{DE}=\frac{AE}{EC}$，
∴CE2=AE•DE．
∴IE2=ED•EA．
点评 本题考查了三角形内心与角平分线的性质、圆的性质、相似三角形的判定与性质定理，考查了推理能力与计算能力，属于中档题．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
4．
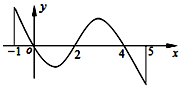已知函数f（x）定义域为[-1，5]，部分对应值如表，f（x）的导函数f′（x）的图象如图所示．
下列关于函数f（x）的命题：
①函数f（x）的极大值点有2个；
②函数f（x）在[0，2]上是减函数；
③若x∈[-1，t]时，f（x）的最大值是2，则t的最大值为4；
④当1＜a＜2时，函数y=f（x）-a有4个零点．
其中是真命题的是①②．（填写序号）
已知函数f（x）定义域为[-1，5]，部分对应值如表，f（x）的导函数f′（x）的图象如图所示．| x | -1 | 0 | 4 | 5 |
| f（x） | 1 | 2 | 2 | 1 |
①函数f（x）的极大值点有2个；
②函数f（x）在[0，2]上是减函数；
③若x∈[-1，t]时，f（x）的最大值是2，则t的最大值为4；
④当1＜a＜2时，函数y=f（x）-a有4个零点．
其中是真命题的是①②．（填写序号）
9．已知Sn为数列{an}的前n项和，若a2=3且Sn+1=2Sn，则a4等于（ ）
| A． | 6 | B． | 12 | C． | 16 | D． | 24 |
13．直线ax+2y+1=0和直线3x+（a-1）y+1=0平行，则a=（ ）
| A． | -2 | B． | 2或-3 | C． | 3 | D． | -2或3 |
10．集合M={y|y=-x2，x∈R}，N={x|x2+y2=2，x∈R}，则M∩N=（ ）
| A． | {（-1，-1），（1，-1）} | B． | {-1} | C． | [-1，0] | D． | [-$\sqrt{2}$，0] |
8．2016年皖智教育联盟第一次联考后，为分析数学考试成绩随机抽取20名同学的成绩统计如下：
（Ⅰ）完成上述表格，并根据上述数据估算这20名职工的平均成绩；
（Ⅱ）若从这20名同学中任选3人，求至少有1人的成绩在90分以上（含90分）的概率；
（Ⅲ）以频率估计概率，若在全部参考同学（假设样本容量为无穷大）中作出这样的测试，且随机抽取3人，记分数在110分以上（含110分）的人数为X，求X的分布列和数学期望．
| 分数段（分） | [50，70） | [70，90） | [90，110） | [110，130） | [130，150] | 总计 |
| 频数 | 2 | 5 | 8 | 3 | 2 | 20 |
| 频率 | 0.10 | 0.25 | 0.40 | 0.15 | 0.10 | 1 |
（Ⅱ）若从这20名同学中任选3人，求至少有1人的成绩在90分以上（含90分）的概率；
（Ⅲ）以频率估计概率，若在全部参考同学（假设样本容量为无穷大）中作出这样的测试，且随机抽取3人，记分数在110分以上（含110分）的人数为X，求X的分布列和数学期望．