题目内容
1.已知四点A(1,7),B(-5,6),C(-4,0),D(2,1),判断四边形ABCD的形状,并说明理由.分析 由$\overrightarrow{AB}$=$\overrightarrow{DC}$得出四边形ABCD是平行四边形;由$\overrightarrow{AC}$•$\overrightarrow{BD}$=0得出平行四边形ABCD是菱形;由|$\overrightarrow{AC}$|=|$\overrightarrow{BD}$|得出菱形ABCD是正方形.
解答 解:四边形ABCD是菱形.
∵A(1,7),B(-5,6),C(-4,0),D(2,1),
∴$\overrightarrow{AB}$=(-6,-1),$\overrightarrow{DC}$=(-6,-1);
∴$\overrightarrow{AB}$=$\overrightarrow{DC}$,即AB∥CD,且AB=CD;
∴四边形ABCD是平行四边形;
又$\overrightarrow{AC}$=(-5,-7),$\overrightarrow{BD}$=(7,-5),
∴$\overrightarrow{AC}$•$\overrightarrow{BD}$=-5×7-7×(-5)=0,
∴$\overrightarrow{AC}$⊥$\overrightarrow{BD}$,
∴平行四边形ABCD是菱形;
又|$\overrightarrow{AC}$|=|$\overrightarrow{BD}$|=$\sqrt{74}$,
∴菱形ABCD是正方形.
点评 本题考查了平面向量的坐标表示,也考查了平面向量的坐标运算问题,是基础题目.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
11.双曲线x2-4y2=8的离心率是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | 2 |
9.二次函数y=(x+1)2+2的顶点是( )
| A. | (1,2) | B. | (1,-2) | C. | (-1,2) | D. | (-1,-2) |
16.函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则( )
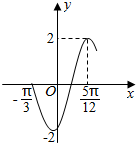
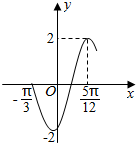
| A. | 函数f(x)的最小正周期是2π | |
| B. | 函数f(x)的图象可由函数g(x)=2sin2x的图象向右平移$\frac{π}{3}$个单位长度得到 | |
| C. | 函数f(x)的图象关于直线x=-$\frac{π}{12}$对称 | |
| D. | 函数f(x)在区间[-$\frac{7π}{12}$+kπ,-$\frac{π}{12}$+kπ](k∈Z)上是增函数 |