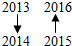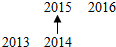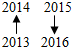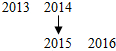题目内容

2．如果复数（m2+i）（1+mi）的虚部为0，则实数m=-1．

分析 化简复数，使虚部为0，可求实数m．

解答 解：复数（m2+i）（1+mi）=（m2-m）+（1+m3）i
∵复数（m2+i）（1+mi）的虚部为0，
∴1+m3=0，
∴m=-1
故答案为：-1．

点评 复数运算，明确分类，本题是基础题．

练习册系列答案
相关题目
12．已知不等式$\frac{x-a}{2-x}$＞0的解集为（-2，2），则不等式x2+x+a＜0的解集为（-2，1）（用区间表示）．
13．已知$\overrightarrow{{A}_{1}{A}_{n}}=2\overrightarrow{a}$，$＜\overrightarrow{a}，\overrightarrow{b}＞$=150°，|$\overrightarrow{a}$|=$\sqrt{3}$，则$\overrightarrow{{A}_{1}{A}_{2}}+\overrightarrow{{A}_{2}{A}_{3}}+…+\overrightarrow{{A}_{n-1}{A}_{n}}$（n＞0，n∈N+）在$\overrightarrow{b}$方向上的投影为$-\frac{3}{2}$．
10．从P（2，3）向圆（x-1）2+（y-1）2=1引切线，则：①切点长为2，②两切点之间距离为$\frac{4\sqrt{5}}{5}$．
17．a、b、c分别表示方程x+log2x=2，x+log3x=2，x+log2x=1的根，则它们的大小关系是（　　）
A．a＞b＞cB．b＞a＞cC．c＞a＞bD．c＞b＞a
7．对于任意实数a、b∈[0，1]，则a、b满足a＜b＜$\sqrt{a}$的概率是（　　）
A．$\frac{1}{4}$B．$\frac{1}{5}$C．$\frac{1}{6}$D．$\frac{1}{7}$
14．函数f（x）=log${\;}_{\frac{1}{2}}$（3x+1）的值域是（-∞，0）．
16．函数f（x）=2sin（ωx+φ）（ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）的部分图象如图所示，则（　　）
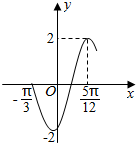
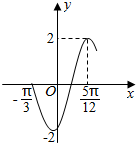
A．函数f（x）的最小正周期是2π
B．函数f（x）的图象可由函数g（x）=2sin2x的图象向右平移$\frac{π}{3}$个单位长度得到
C．函数f（x）的图象关于直线x=-$\frac{π}{12}$对称
D．函数f（x）在区间[-$\frac{7π}{12}$+kπ，-$\frac{π}{12}$+kπ]（k∈Z）上是增函数
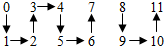17．数0，1，2，3，4，5，…按以下规律排列： …，则从2013到2016四数之间的位置图形为（　　）
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网