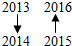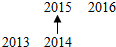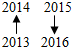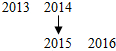题目内容
8.过(1,1)作直线与抛物线y2=x只有一个公共点,这样的直线有( )| A. | 4条 | B. | 3条 | C. | 2条 | D. | 1条 |
分析 判断点(1,1)与抛物线的位置关系,从而得到结论.
解答 解:抛物线y2=x的焦点为($\frac{1}{4}$,0),(1,1)点在抛物线上,
①当过点(1,1)的直线的斜率等于0时,直线的方程为 y=1,与抛物线y2=x的轴平行,只有一个公共点.
②过点(1,1)与抛物线y2=x相切的直线与该抛物线只有一个公共点.
故选:C.
点评 本题考查直线和圆锥曲线的位置关系,是解题的关键.基本知识的考查.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则( )
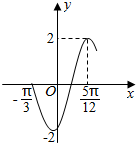
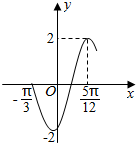
| A. | 函数f(x)的最小正周期是2π | |
| B. | 函数f(x)的图象可由函数g(x)=2sin2x的图象向右平移$\frac{π}{3}$个单位长度得到 | |
| C. | 函数f(x)的图象关于直线x=-$\frac{π}{12}$对称 | |
| D. | 函数f(x)在区间[-$\frac{7π}{12}$+kπ,-$\frac{π}{12}$+kπ](k∈Z)上是增函数 |
18.下列命题中,正确的命题是( )
| A. | 若a>b,c>d,则ac>bd | B. | 若$\frac{1}{a}>\frac{1}{b}$,则 a<b | ||
| C. | 若b>c,则|a|b≥|a|c | D. | 若a>b,c>d,则a-c>b-d |
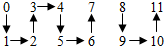 …,则从2013到2016四数之间的位置图形为( )
…,则从2013到2016四数之间的位置图形为( )