题目内容

4．已知等差数列{an}的首项a1=1，公差d≠0，且a2是a1与a4的等比中项，则d=（　　）
A．1B．2C．3D．4

分析 由题意可得${{a}_{2}}^{2}={a}_{1}•{a}_{4}$，把a2、a4用含有d的代数式表示，求解关于d的方程得答案．

解答 解：由a2是a1与a4的等比中项，得
${{a}_{2}}^{2}={a}_{1}•{a}_{4}$，即$（{a}_{1}+d）^{2}={a}_{1}（{a}_{1}+3d）$，
又a1=1，
∴（d+1）2=3d+1，
又d≠0，解得：d=1．
故选：A．

点评 本题考查等差数列的通项公式，考查了等比数列的性质，是基础的计算题．

练习册系列答案
相关题目
9．二次函数y=（x+1）2+2的顶点是（　　）
A．（1，2）B．（1，-2）C．（-1，2）D．（-1，-2）
10．从P（2，3）向圆（x-1）2+（y-1）2=1引切线，则：①切点长为2，②两切点之间距离为$\frac{4\sqrt{5}}{5}$．
7．对于任意实数a、b∈[0，1]，则a、b满足a＜b＜$\sqrt{a}$的概率是（　　）
A．$\frac{1}{4}$B．$\frac{1}{5}$C．$\frac{1}{6}$D．$\frac{1}{7}$
14．函数f（x）=log${\;}_{\frac{1}{2}}$（3x+1）的值域是（-∞，0）．
9．设a，b，c为三角形ABC三边，a≠1，b＜c，若logc+ba+logc-ba=2logc+balog c-ba，则三角形ABC的形状为（　　）
A．锐角三角形B．直角三角形C．钝角三角形D．无法确定
16．函数f（x）=2sin（ωx+φ）（ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）的部分图象如图所示，则（　　）
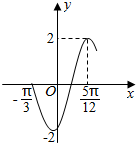
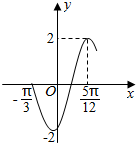
A．函数f（x）的最小正周期是2π
B．函数f（x）的图象可由函数g（x）=2sin2x的图象向右平移$\frac{π}{3}$个单位长度得到
C．函数f（x）的图象关于直线x=-$\frac{π}{12}$对称
D．函数f（x）在区间[-$\frac{7π}{12}$+kπ，-$\frac{π}{12}$+kπ]（k∈Z）上是增函数
13．一个几何体的三视图如图所示（单位长度：cm），则此几何体的表面积是24+2$\sqrt{5}$
14．已知圆x2+y2-2x+my-4=0上两点M，N关于直线2x+y=0对称，则圆的方程为（　　）
A．（x-1）2+（y+2）2=3B．（x-1）2+（y+2）2=9C．（x-1）2+（y-2）2=4D．（x-1）2+（y-2）2=12

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网