题目内容
已知函数f(x)=
,x∈[1,+∞),当a=-
时,求函数的最小值.
| x2+2x+a |
| x |
| 1 |
| 2 |
考点:函数的最值及其几何意义
专题:计算题,函数的性质及应用,导数的综合应用
分析:化简f(x)=
=x-
+2,再求导f′(x)=1+
>0;从而确定单调性及最值.
x2+2x-
| ||
| x |
| 1 |
| 2x |
| 1 |
| 2x2 |
解答:
解:当a=-
时,
f(x)=
=x-
+2,
f′(x)=1+
>0;
故f(x)=
在[1,+∞)上是增函数,
fmin(x)=1-
+2=
.
| 1 |
| 2 |
f(x)=
x2+2x-
| ||
| x |
| 1 |
| 2x |
f′(x)=1+
| 1 |
| 2x2 |
故f(x)=
x2+2x-
| ||
| x |
fmin(x)=1-
| 1 |
| 2 |
| 5 |
| 2 |
点评:本题考查了导数的综合应用及函数的最值,属于基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
双曲线
-
=1的渐近线方程为( )
| x2 |
| 4 |
| y2 |
| 12 |
| A、x=±2 | ||
B、y=±2
| ||
C、y=±
| ||
D、x=±
|
已知tanα=4,
=
,则则tan(α+β)=( )
| 1 |
| tanβ |
| 1 |
| 3 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
对a,b∈R,记max{a,b}=
,则函数f(x)=max{|x+1|,x2-2x+
}( )
|
| 9 |
| 4 |
A、有最大值
| ||
B、有最大值
| ||
C、有最小值
| ||
D、有最小值
|
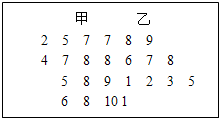 在某次考试中,从甲乙两个班各抽取10名学生的数学成绩进行统计分析,两个班成绩的茎叶图如图所示,成绩不小于90分的为及格.
在某次考试中,从甲乙两个班各抽取10名学生的数学成绩进行统计分析,两个班成绩的茎叶图如图所示,成绩不小于90分的为及格.