题目内容

弹子跳棋共有60颗大小相同的球形弹子，现在在棋盘上将他们叠成正四面体球堆，试剩下的弹子尽可能的少，那么剩余的弹子共有（　　）颗．
A、11B、4C、5D、0
考点：进行简单的演绎推理
专题：综合题,推理和证明
分析：正四面体的特征和题设构造过程，第k层为k个连续自然数的和，求出前k层的个数，即可得出结论．
解答： 解：依题设第k层正四面体为1+2+…+k=
k2+k
2
，
则前k层共有
1
2
（12+22+…+k2）+
1
2
（1+2+…+k）=
k(k+1)(k+2)
6
≤60
∴k最大为6，剩4，
故选B．
点评：本题考查进行简单的演绎推理，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
已知函数f(x)=ln(x+
x2+1
)满足f（a-1）+f（b-3）=0，则a+b=
 
．
若以F为右焦点的双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的左支上存在一点P，使得线段PF被y=
b
a
x垂直平分，则双曲线的离心率是
 
．
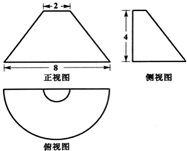如图是某几何体的三视图（单位：cm），正视图是等腰梯形，俯视图中的曲线是两个同心的半圆，侧视图是直角梯形．则该几何体的体积等于
 
cm3，它的表面积等于
 
cm2．
在△ABC中，AC边上的高BD所在直线方程为2x+y-3=0，∠CAB的角平分线所在直线方程为y=1，若点C坐标为（3，3）．
（Ⅰ）求直线AC的方程和点A的坐标；
（Ⅱ）求点B的坐标．
学校为了解同学们对年段和班级管理的满意程度，通过问卷调查了高一年的学生、高二年的学生、高三年的学生共250人，结果如下表：
高一年的学生高二年的学生高三年的学生
满意78y75
不满意12z5
（Ⅰ）现用分层抽样的方法在所调查的人员中抽取25人，则高二年的学生应抽取多少人？
（Ⅱ）若y≥70，z≥2，求问卷调查中同学们对年段和班级管理的满意度不小于0.9的概率．
（注：满意度=
满意人数
总人数
）
（Ⅲ）若高三年级的某班级中的10个学生中有2个对年段和班级的管理不满意，老师从这10个学生中随机选择2个学生进行问卷调查，求这2个学生中对年段和班级的管理不满意的人数ξ的期望．
已知函数f（x）=
x2+2x+a
x
，x∈[1，+∞），当a=-
1
2
时，求函数的最小值．
某校为了响应《中共中央国务院关于加强青少年体育增强青少年体质的意见》精神，落实“生命-和谐”教育理念和阳光体育行动的现代健康理念，学校特组织“踢毽球”大赛，某班为了选出一人参加比赛，对班上甲乙两位同学进行了8次测试，且每次测试之间是相互独立．成绩如下：（单位：个/分钟）
甲8081937288758384
乙8293708477877885
（1）用茎叶图表示这两组数据
（2）从统计学的角度考虑，你认为选派那位学生参加比赛合适，请说明理由？
（3）若将频率视为概率，对甲同学在今后的三次比赛成绩进行预测，记这三次成绩高于79个/分钟的次数为ξ，求ξ的分布列及数学期望Eξ．
（参考数据：22+12+112+102+62+72+12+22=316，02+112+122+22+52+52+42+32=344）
数列{an}是等差数列，若a1+1，a3+2，a5+3构成公比为q的等比数列，则q=（　　）
A、1B、2C、3D、4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网