题目内容
11.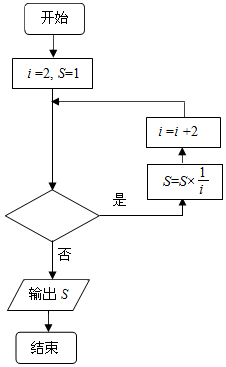 如图,给出的是计算$\frac{1}{2}$×$\frac{1}{4}$×$\frac{1}{6}$×…×$\frac{1}{2016}$的值的程序框图,其中判断框内不能填入的是( )
如图,给出的是计算$\frac{1}{2}$×$\frac{1}{4}$×$\frac{1}{6}$×…×$\frac{1}{2016}$的值的程序框图,其中判断框内不能填入的是( )| A. | i≤2017? | B. | i<2018? | C. | i≤2015? | D. | i≤2016? |
分析 根据程序运行后输出的算式,分析倒数第一圈,即i=2016时满足条件,i=2018不满足循环条件;由此可得判断框内不能填入的选项.
解答 解:∵程序运行后输出的是S=$\frac{1}{2}$×$\frac{1}{4}$×$\frac{1}{6}$×…×$\frac{1}{2016}$的值,
∴分析倒数第一圈,i=2016时,满足条件,执行循环S=$\frac{1}{2}$×$\frac{1}{4}$×$\frac{1}{6}$×…×$\frac{1}{2016}$,
i=i+2=2018,此时不满足条件,终止循环,输出S=$\frac{1}{2}$×$\frac{1}{4}$×$\frac{1}{6}$×…×$\frac{1}{2016}$的值;
∴判断框内能填入“i≤2017?”,“i<2018?”,“i≤2016?”,
不能填入“i≤2015?”.
故选:C.
点评 本题考查了程序框图中的当型循环问题,解题的关键是分析倒数第一圈,是基础题目.

练习册系列答案
相关题目
1.已知命题p:?x∈(0,$\frac{π}{2}}$),sinx<x,则( )
| A. | p是真命题,¬p:?x∈(0,$\frac{π}{2}}$),sinx≥x | B. | p是真命题,¬p:?x0∈(0,$\frac{π}{2}}$),sinx0≥x0 | ||
| C. | p是假命题,¬p:?x∈(0,$\frac{π}{2}}$),sinx≥x | D. | p是假命题,¬p:?x0∈(0,$\frac{π}{2}}$),sinx0≥x0 |
2.i为虚数单位,则复数$\frac{3-2i}{i}$=( )
| A. | 2-3i | B. | -2-3i | C. | 3-2i | D. | -2+3i |
6.设全集为R,集合A={x|$\frac{1-x}{1+x}$≥0},B={x|-2≤x<0},则(∁RA)∩B=( )
| A. | (-1,0) | B. | [-1,0) | C. | [-2,-1] | D. | [-2,-1) |
3.“a>2且b>2”是“ab>4”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
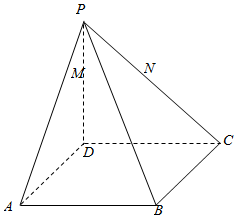 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,M,N分别为PD,PC上的点,且$\frac{PM}{MD}$=$\frac{PN}{NC}$,求证:MN∥AB.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,M,N分别为PD,PC上的点,且$\frac{PM}{MD}$=$\frac{PN}{NC}$,求证:MN∥AB.