题目内容
1.已知命题p:?x∈(0,$\frac{π}{2}}$),sinx<x,则( )| A. | p是真命题,¬p:?x∈(0,$\frac{π}{2}}$),sinx≥x | B. | p是真命题,¬p:?x0∈(0,$\frac{π}{2}}$),sinx0≥x0 | ||
| C. | p是假命题,¬p:?x∈(0,$\frac{π}{2}}$),sinx≥x | D. | p是假命题,¬p:?x0∈(0,$\frac{π}{2}}$),sinx0≥x0 |
分析 令f(x)=sinx-x,求出f(x)的单调性,从而判断出sinx<x,得到命题p是真命题,由命题的否定的定义,要否定命题的结论,同时改变量词,得到¬p.
解答 解:令f(x)=sinx-x,则f′(x)=cosx-1<0,
函数f(x)在(0,$\frac{π}{2}$)递减,
f(x)max<f(0)=0,
故sinx<x,命题p是真命题,
由命题的否定的定义,要否定命题的结论,同时改变量词知
¬p:?x0∈(0,$\frac{π}{2}$),sinx0≥x0,
故选:B.
点评 本题考查一个命题的否定的定义,考查函数的单调性问题,是一道基础题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
16.已知等差数列{an}满足a4-a2=2,且a1,a3,a7成等比数列.
(Ⅰ)求{an}的通项公式;
(Ⅱ)设bn=$\frac{1}{{{a}_{n}}^{2}-1}$,求数列{bn}的前n项和.
(Ⅰ)求{an}的通项公式;
(Ⅱ)设bn=$\frac{1}{{{a}_{n}}^{2}-1}$,求数列{bn}的前n项和.
11.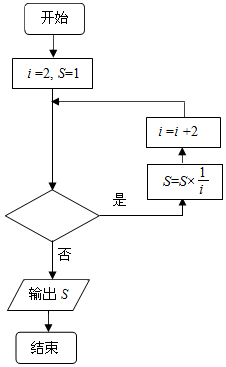 如图,给出的是计算$\frac{1}{2}$×$\frac{1}{4}$×$\frac{1}{6}$×…×$\frac{1}{2016}$的值的程序框图,其中判断框内不能填入的是( )
如图,给出的是计算$\frac{1}{2}$×$\frac{1}{4}$×$\frac{1}{6}$×…×$\frac{1}{2016}$的值的程序框图,其中判断框内不能填入的是( )
 如图,给出的是计算$\frac{1}{2}$×$\frac{1}{4}$×$\frac{1}{6}$×…×$\frac{1}{2016}$的值的程序框图,其中判断框内不能填入的是( )
如图,给出的是计算$\frac{1}{2}$×$\frac{1}{4}$×$\frac{1}{6}$×…×$\frac{1}{2016}$的值的程序框图,其中判断框内不能填入的是( )| A. | i≤2017? | B. | i<2018? | C. | i≤2015? | D. | i≤2016? |