题目内容
6．设全集为R，集合A={x|$\frac{1-x}{1+x}$≥0}，B={x|-2≤x＜0}，则（∁RA）∩B=（ ）| A． | （-1，0） | B． | [-1，0） | C． | [-2，-1] | D． | [-2，-1） |
分析 先解出关于集合A的不等式，求出A的补集，从而求出其补集与B的交集．
解答 解：∵集合A={x|$\frac{1-x}{1+x}$≥0}={x|-1＜x≤1}=（-1，1]，
∴∁RA=（-∞，-1]∪（1，+∞），
∵B={x|-2≤x＜0}=[-2，0）
∴（∁RA）∩B=[-1，0）
故选：B．
点评 本题考查了集合的混合运算，是一道基础题．
练习册系列答案
相关题目
16．已知等差数列{an}满足a4-a2=2，且a1，a3，a7成等比数列．
（Ⅰ）求{an}的通项公式；
（Ⅱ）设bn=$\frac{1}{{{a}_{n}}^{2}-1}$，求数列{bn}的前n项和．
（Ⅰ）求{an}的通项公式；
（Ⅱ）设bn=$\frac{1}{{{a}_{n}}^{2}-1}$，求数列{bn}的前n项和．
11．
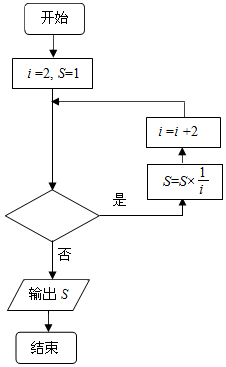如图，给出的是计算$\frac{1}{2}$×$\frac{1}{4}$×$\frac{1}{6}$×…×$\frac{1}{2016}$的值的程序框图，其中判断框内不能填入的是（ ）
如图，给出的是计算$\frac{1}{2}$×$\frac{1}{4}$×$\frac{1}{6}$×…×$\frac{1}{2016}$的值的程序框图，其中判断框内不能填入的是（ ）| A． | i≤2017？ | B． | i＜2018？ | C． | i≤2015？ | D． | i≤2016？ |
已知点Q是抛物线C：y2=2px（p＞0）上的动点，点Q到抛物线准线与到点P（-$\frac{1}{2}$，1）的距离之和的最小值为$\sqrt{2}$．