题目内容
16.在△ABC中,内角A,B,C的对边分别为a,b,c,已知$\frac{sinB}{sinA+sinC}$=1-$\frac{sinC}{sinA+sinB}$,且b=5,acosC=-1.(1)求角A;
(2)求△ABC的面积.
分析 (1)先化简,再根据正弦定理和余弦定理即可求出A的值;
(2)由余弦定理和b=5,acosC=-1,求出c,再根据三角面积公式即可求出.
解答 解:(1)在△ABC中,∵$\frac{sinB}{sinA+sinC}$=1-$\frac{sinC}{sinA+sinB}$,
∴sinB(sinA+sinB)=(sinA+sinC)(sinA+sinB)-sinC(sinA+sinC),
∴sin2B=sin2A+sinCsinB-sin2C,
由正弦定理,
∴b2=a2-c2+bc,
即bc=b2+c2-a2,
由余弦定理可得cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2ac}$=$\frac{1}{2}$,
∵0<A<π,
∴A=$\frac{π}{3}$,
(2)由余弦定理得cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{2{b}^{2}-bc}{2ab}$=$\frac{2b-c}{2a}$=-$\frac{1}{a}$,
∴c-2b=2,
∴c=2b+2=12,
∴S△ABC=$\frac{1}{2}$bcsinA=$\frac{1}{2}×5×12×\frac{\sqrt{3}}{2}$=15$\sqrt{3}$.
点评 本题考查了正弦定理,余弦定理,三角形的面积公式,关键是灵活应用这些定理,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.设x,y满足约束条件$\left\{\begin{array}{l}x≤1\\ x-2y≥0\\ y-2≤0\end{array}\right.$,则z=x-2y-3的最小值为( )
| A. | -6 | B. | -3 | C. | -1 | D. | 1 |
4.已知双曲线C的左右焦点分别为F1、F2,且F2恰为抛物线y2=8x的焦点.设A为双曲线C与该抛物线的一个交点,若△AF1F2是以AF1的底边的等腰三角形,则双曲线C的离心率为( )
| A. | 1+$\sqrt{3}$ | B. | 1+$\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
11.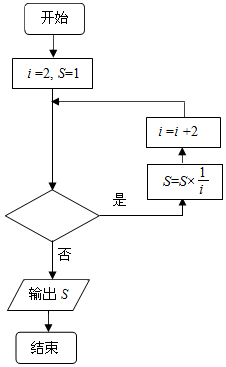 如图,给出的是计算$\frac{1}{2}$×$\frac{1}{4}$×$\frac{1}{6}$×…×$\frac{1}{2016}$的值的程序框图,其中判断框内不能填入的是( )
如图,给出的是计算$\frac{1}{2}$×$\frac{1}{4}$×$\frac{1}{6}$×…×$\frac{1}{2016}$的值的程序框图,其中判断框内不能填入的是( )
 如图,给出的是计算$\frac{1}{2}$×$\frac{1}{4}$×$\frac{1}{6}$×…×$\frac{1}{2016}$的值的程序框图,其中判断框内不能填入的是( )
如图,给出的是计算$\frac{1}{2}$×$\frac{1}{4}$×$\frac{1}{6}$×…×$\frac{1}{2016}$的值的程序框图,其中判断框内不能填入的是( )| A. | i≤2017? | B. | i<2018? | C. | i≤2015? | D. | i≤2016? |
1.设复数z=$\frac{1-i}{1+i}$(i为虚数单位),则z=( )
| A. | i | B. | -i | C. | 2i | D. | -2i |