题目内容
20.设x∈(0,$\frac{π}{2}$],则下列命题:(1)x≥sinx;(2)sinx≥xcosx;(3)y=$\frac{sinx}{x}$是单调减函数;(4)若sinkx≥ksinx恒成立,则正数k的取值范围是0<k≤1;其中真命题的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据函数的单调性,分别对(1),(2),(3),(4)进行判断即可.
解答 解:设x∈(0,$\frac{π}{2}$],则下列命题:
(1)令f(x)=x-sinx,则f′(x)=1-cosx≥0,
∴f(x)min>f(0)=0,故x>sinx,故x≥sinx;
(2)令f(x)=sinx-xcosx,则f′(x)=cosx-(cosx-xsinx)=xsinx>0,
f(x)递增,f(x)min>f(0)=0,sinx>xcosx,故sinx≥xcosx;
(3)∵y=$\frac{sinx}{x}$,∴y′=$\frac{xcosx-sinx}{{x}^{2}}$,
令g(x)=xcosx-sinx,g′(x)=-sinx<0,
∴g(x)max<g(0)=0,
∴y′<0
∴y=$\frac{sinx}{x}$是单调减函数;
(4)若sinkx≥ksinx恒成立,
而0<sinkx≤1,0<sinx≤1
则正数k的取值范围是0<k≤1;
其中真命题的个数是4个,
故选:D.
点评 本题考查了函数的单调性问题,考查导数的应用,是一道中档题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
11.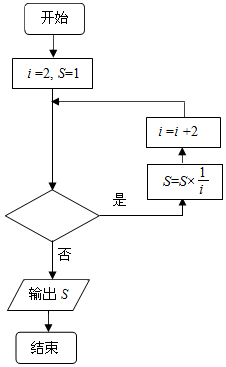 如图,给出的是计算$\frac{1}{2}$×$\frac{1}{4}$×$\frac{1}{6}$×…×$\frac{1}{2016}$的值的程序框图,其中判断框内不能填入的是( )
如图,给出的是计算$\frac{1}{2}$×$\frac{1}{4}$×$\frac{1}{6}$×…×$\frac{1}{2016}$的值的程序框图,其中判断框内不能填入的是( )
 如图,给出的是计算$\frac{1}{2}$×$\frac{1}{4}$×$\frac{1}{6}$×…×$\frac{1}{2016}$的值的程序框图,其中判断框内不能填入的是( )
如图,给出的是计算$\frac{1}{2}$×$\frac{1}{4}$×$\frac{1}{6}$×…×$\frac{1}{2016}$的值的程序框图,其中判断框内不能填入的是( )| A. | i≤2017? | B. | i<2018? | C. | i≤2015? | D. | i≤2016? |