题目内容
 已知一棱锥的三视图如图所示,其中侧视图和俯视图都是等腰直角三角形,正视图为直角梯形,则该棱锥的体积为( )
已知一棱锥的三视图如图所示,其中侧视图和俯视图都是等腰直角三角形,正视图为直角梯形,则该棱锥的体积为( )| A、8 | B、16 | C、32 | D、48 |
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由已知中的三视图可得该几何体是以底面为直角梯形的四棱锥,求出底面面积和高,代入可得答案.
解答:
解:该几何体是以底面为直角梯形的四棱锥,
底面面积S=
×(2+4)×4=12,
高h=4,
故体积V=
×S×h=16.
故选:B
底面面积S=
| 1 |
| 2 |
高h=4,
故体积V=
| 1 |
| 3 |
故选:B
点评:本题考查的知识点是由三视图求体积,其中根据已知的三视图判断出几何体的形状是解答的关键.

练习册系列答案
相关题目
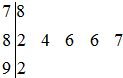 如图是2010年元旦晚会举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的方差为( )
如图是2010年元旦晚会举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的方差为( )| A、4.84 | B、0.8 |
| C、1.6 | D、3.2 |
 茎叶图记录了甲、乙两组各6名学生在一次数学测试中的成绩(单位:分).已知甲组数据的众数为124,乙组数据的平均数即为甲组数据的中位数,则x、y的值分别为( )
茎叶图记录了甲、乙两组各6名学生在一次数学测试中的成绩(单位:分).已知甲组数据的众数为124,乙组数据的平均数即为甲组数据的中位数,则x、y的值分别为( )| A、4、5 | B、5、4 |
| C、4、4 | D、5、5 |
若一元二次不等式f(x)>0的解集为{x|-2<x<1},则f(2x)<0的解集为( )
| A、{x|x<-2或x>0} |
| B、{x|x<0或x>2} |
| C、{x|x>0} |
| D、{x|x<0} |
已知函数f(x)=x+
,若对任意x∈N*,都有f(x)≥f(3),则实数c的取值范围是( )
| c |
| x |
| A、[3,+∞) |
| B、{9} |
| C、[3,9] |
| D、[6,12] |
若(
-x
)n展开式中含有x2项,则n的最小值是( )
| 1 |
| x |
| x |
| A、15 | B、8 | C、7 | D、3 |
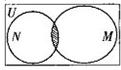 已知全集U=R,集合M={x|-2≤x-1≤2}和N={x|x=2k-1,k=1,2,…}的关系的韦恩(Venn)图如图所示,则阴影部分所示的集合的元素共有
已知全集U=R,集合M={x|-2≤x-1≤2}和N={x|x=2k-1,k=1,2,…}的关系的韦恩(Venn)图如图所示,则阴影部分所示的集合的元素共有