题目内容
13. 函数f(x)=sin(ωx+φ)(其中|φ|<$\frac{π}{2}$)的图象如图所示,为了得到y=cosωx的图象,只需把y=f(x)的图象( )
函数f(x)=sin(ωx+φ)(其中|φ|<$\frac{π}{2}$)的图象如图所示,为了得到y=cosωx的图象,只需把y=f(x)的图象( )| A. | 向右平移$\frac{π}{6}$个单位长度 | B. | 向左平移$\frac{π}{6}$个单位长度 | ||
| C. | 向右平移$\frac{π}{12}$个单位长度 | D. | 向左平移$\frac{π}{12}$个单位长度 |
分析 利用图象的最低点确定A的值,利用周期确定ω,再根据图象过点($\frac{π}{3}$,0),确定φ的值,即可求函数f(x)的解析式,由y=cos2x=sin[2(x+$\frac{π}{6}$+$\frac{π}{12}$)],根据图象的变换规律即可得解.
解答 解:∵T=4×($\frac{7}{12}$$π-\frac{π}{3}$)=π,
∴ω=2,
∴f(x)=sin(2x+φ),π
∵图象过点($\frac{π}{3}$,0),
∴sin(2×$\frac{π}{3}$+φ)=0,
∵|φ|<$\frac{π}{2}$,∴φ=$\frac{π}{3}$,
∴f(x)=sin(2x+$\frac{π}{3}$)=sin[2(x+$\frac{π}{6}$)];
∵y=cos2x=sin(2x+$\frac{π}{2}$)=sin[2(x+$\frac{π}{4}$)]=sin[2(x+$\frac{π}{6}$+$\frac{π}{12}$)];
∴函数f(x)的图象向左平移$\frac{π}{12}$个单位长度,可以得到函数y=sin2x的图象.
故选:D.
点评 本题考查三角函数解析式的确定,考查图象的变换,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.设a>0,b>0( )
| A. | 若lna+2a=lnb+3b,则a>b | B. | 2a+2a=2b+3b,则a<b | ||
| C. | 若lna-2a=lnb-3b,则a>b | D. | 2a-2a=2b-3b,则a<b |
5.已知平面向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为$\frac{π}{3}$,且|$\overrightarrow{b}$|=1,|$\overrightarrow{a}$+2$\overrightarrow{b}$|=2$\sqrt{3}$,则|$\overrightarrow{a}$|=( )
| A. | 2 | B. | $\sqrt{3}$ | C. | 1 | D. | 3 |
3.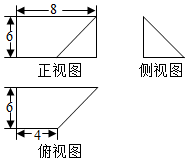 一个几何体的三视图如图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则这个几何体的体积是( )
一个几何体的三视图如图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则这个几何体的体积是( )
 一个几何体的三视图如图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则这个几何体的体积是( )
一个几何体的三视图如图所示,其中正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则这个几何体的体积是( )| A. | 72 | B. | 80 | C. | 120 | D. | 144 |