题目内容
8.已知|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°,若m$\overrightarrow{a}$+3$\overrightarrow{b}$与2$\overrightarrow{a}$-m$\overrightarrow{b}$垂直,则实数m的值为( )| A. | 0 | B. | 6或-6 | C. | 1或-6 | D. | 6或-1 |
分析 根据向量的数量运算和向量垂直的条件计算即可.
解答 解:∵m$\overrightarrow{a}$+3$\overrightarrow{b}$与2$\overrightarrow{a}$-m$\overrightarrow{b}$垂直,
∴(m$\overrightarrow{a}$+3$\overrightarrow{b}$)•(2$\overrightarrow{a}$-m$\overrightarrow{b}$)=2m|$\overrightarrow{a}$|2-3m|$\overrightarrow{b}$|2+(6-m2)$\overrightarrow{a}•\overrightarrow{b}$=8m-3m+(6-m2)•2×1×$\frac{1}{2}$=0,
即m2-5m-6=0,
解得m=6或m=-1,
故选:D.
点评 本题考查了向量的数量运算和向量垂直的条件,属于基础题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
18.已知集合A={0,1},B={-1,0,a+2},且A⊆B,则实数a=( )
| A. | 0 | B. | -1 | C. | -2 | D. | -3 |
13. 函数f(x)=sin(ωx+φ)(其中|φ|<$\frac{π}{2}$)的图象如图所示,为了得到y=cosωx的图象,只需把y=f(x)的图象( )
函数f(x)=sin(ωx+φ)(其中|φ|<$\frac{π}{2}$)的图象如图所示,为了得到y=cosωx的图象,只需把y=f(x)的图象( )
 函数f(x)=sin(ωx+φ)(其中|φ|<$\frac{π}{2}$)的图象如图所示,为了得到y=cosωx的图象,只需把y=f(x)的图象( )
函数f(x)=sin(ωx+φ)(其中|φ|<$\frac{π}{2}$)的图象如图所示,为了得到y=cosωx的图象,只需把y=f(x)的图象( )| A. | 向右平移$\frac{π}{6}$个单位长度 | B. | 向左平移$\frac{π}{6}$个单位长度 | ||
| C. | 向右平移$\frac{π}{12}$个单位长度 | D. | 向左平移$\frac{π}{12}$个单位长度 |
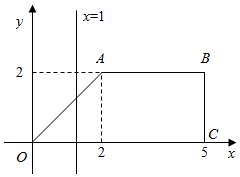 如图,直角梯形OABC位于直线x=t(0≤t≤5)右侧的图形面积为f(t).
如图,直角梯形OABC位于直线x=t(0≤t≤5)右侧的图形面积为f(t).