题目内容
18．在平面直角坐标系中，角α的终边过点P（1，2），则cos2α+sin2α的值为1．分析 利用任意角三角函数的定义和二倍角公式求解．
解答 解：∵在平面直角坐标系中，角α的终边过点P（1，2），
∴x=1，y=2，r=$\sqrt{1+4}=\sqrt{5}$，
∴sinα=$\frac{2}{\sqrt{5}}=\frac{2\sqrt{5}}{5}$，cosα=$\frac{1}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$，
∴cos2α+sin2α=（$\frac{\sqrt{5}}{5}$）2+2sinαcosα=$\frac{1}{5}+2×\frac{2\sqrt{5}}{5}×\frac{\sqrt{5}}{5}$=1．
故答案为：1．
点评 本题考查三角函数化简求值，是基础题，解题时要认真审题，注意任意角三角函数的定义和二倍角公式的合理运用．
练习册系列答案
相关题目
14．已知数列{an}的前n项的和为Sn，则Sn=2n2-3n是数列{an}为等比数列的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
6．已知|$\overrightarrow a$|=|$\overrightarrow b$|=1，|$\overrightarrow a$-$\overrightarrow b$|=$\sqrt{2}$，则|$\overrightarrow a$+$\overrightarrow b$|=（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | 2 |
13．
函数f（x）=sin（ωx+φ）（其中|φ|＜$\frac{π}{2}$）的图象如图所示，为了得到y=cosωx的图象，只需把y=f（x）的图象（ ）
函数f（x）=sin（ωx+φ）（其中|φ|＜$\frac{π}{2}$）的图象如图所示，为了得到y=cosωx的图象，只需把y=f（x）的图象（ ）| A． | 向右平移$\frac{π}{6}$个单位长度 | B． | 向左平移$\frac{π}{6}$个单位长度 | ||
| C． | 向右平移$\frac{π}{12}$个单位长度 | D． | 向左平移$\frac{π}{12}$个单位长度 |
3．在某学校进行的一次语文与历史成绩中，随机抽取了25位考生的成绩进行分析，25位考生的语文成绩已经统计在茎叶图中，历史成绩如下：
85 52 64 49 55 71 90 66 46 66 39 61 56
78 67 77 58 73 42 80 72 67 70 51 65
（Ⅰ）请根据数据在茎叶图中完成历史成绩统计；
（Ⅱ）请根据数据完成语文成绩的频数分布表及语文成绩的频率分布直方图；
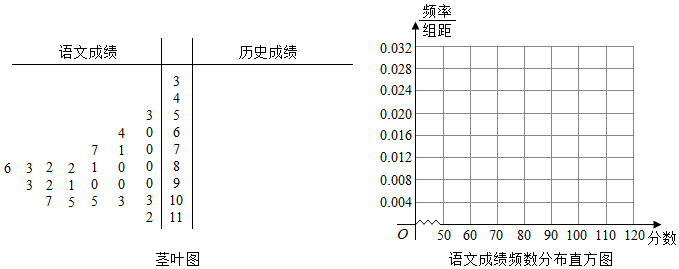
语文成绩的频数分布表：
（Ⅲ）设上述样本中第i位考生的语文、历史成绩分别为xi，yi（i=1，2，…，25）．通过对样本数据进行初步处理发现：语文、历史成绩具有线性相关关系，得到：
$\overline{x}$=$\frac{1}{25}$$\sum_{i=1}^{25}$xi=86，$\overline{y}$=$\frac{1}{25}$$\sum_{i=1}^{25}$yi=64，$\sum_{i=1}^{25}$（xi-$\overline{x}$）（yi-$\overline{y}$）=4698，$\sum_{i=1}^{25}$（xi-$\overline{x}$）2=5524，$\frac{4698}{5524}$≈0.85．
①求y关于x的线性回归方程；
②并据此预测，当某考生的语文成绩为100分时，该生历史成绩．（精确到0.1分）
附：回归直线方程的斜率和截距的最小二乘法估计公式分别为：
$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}•{y}_{i}-\overline{n}x•\overline{y}}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$．
85 52 64 49 55 71 90 66 46 66 39 61 56
78 67 77 58 73 42 80 72 67 70 51 65
（Ⅰ）请根据数据在茎叶图中完成历史成绩统计；
（Ⅱ）请根据数据完成语文成绩的频数分布表及语文成绩的频率分布直方图；
语文成绩的频数分布表：
| 语文成绩分组 | [50，60） | [60，70） | [70，80） | [90，100） | [100，110） | [110，120] |
| 频数 |
$\overline{x}$=$\frac{1}{25}$$\sum_{i=1}^{25}$xi=86，$\overline{y}$=$\frac{1}{25}$$\sum_{i=1}^{25}$yi=64，$\sum_{i=1}^{25}$（xi-$\overline{x}$）（yi-$\overline{y}$）=4698，$\sum_{i=1}^{25}$（xi-$\overline{x}$）2=5524，$\frac{4698}{5524}$≈0.85．
①求y关于x的线性回归方程；
②并据此预测，当某考生的语文成绩为100分时，该生历史成绩．（精确到0.1分）
附：回归直线方程的斜率和截距的最小二乘法估计公式分别为：
$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}•{y}_{i}-\overline{n}x•\overline{y}}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$．
10．如果复数z=$\frac{3-i}{2+i}$（i为虚数单位），则|z|=（ ）
| A． | 1 | B． | 4 | C． | 2 | D． | $\sqrt{2}$ |
7．设函数f（x）=$\left\{\begin{array}{l}{lo{g}_{2}x，x＞0}\\{lo{g}_{\frac{1}{2}}（-x），x＜0}\end{array}\right.$，则f（x）（ ）
| A． | 为奇函数且有（-∞，0）上为增函数 | B． | 为偶函数且有（-∞，0）上为增函数 | ||
| C． | 为奇函数且有（-∞，0）上为减函数 | D． | 为偶函数且有（-∞，0）上为减函数 |