题目内容
9.已知等差数列{an}的前n项和为Sn,a5=12,a20=-18.(1)求数列{an}的通项公式;
(2)数列{an}的前多少项之和最大?求此最大值.
分析 (1)利用等差数列的通项公式即可得出;
(2)由an≥0,解得n即可得出.
解答 解:(1)设等差数列{an}的公差为d,∵a5=12,a20=-18.
∴$\left\{\begin{array}{l}{{a}_{1}+4d=12}\\{{a}_{1}+19d=-18}\end{array}\right.$,解得a1=20,d=-2.
∴an=20-2(n-1)=22-2n.
(2)由an=22-2n≥0,解得n≤11,
∴数列{an}的前10,或11项之和最大.
∴S11=$\frac{11×(20+0)}{2}$=110.
点评 本题考查了等差数列的通项公式及其前n项和公式、数列的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.已知数列{an}的前n项的和为Sn,则Sn=2n2-3n是数列{an}为等比数列的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
13. 函数f(x)=sin(ωx+φ)(其中|φ|<$\frac{π}{2}$)的图象如图所示,为了得到y=cosωx的图象,只需把y=f(x)的图象( )
函数f(x)=sin(ωx+φ)(其中|φ|<$\frac{π}{2}$)的图象如图所示,为了得到y=cosωx的图象,只需把y=f(x)的图象( )
 函数f(x)=sin(ωx+φ)(其中|φ|<$\frac{π}{2}$)的图象如图所示,为了得到y=cosωx的图象,只需把y=f(x)的图象( )
函数f(x)=sin(ωx+φ)(其中|φ|<$\frac{π}{2}$)的图象如图所示,为了得到y=cosωx的图象,只需把y=f(x)的图象( )| A. | 向右平移$\frac{π}{6}$个单位长度 | B. | 向左平移$\frac{π}{6}$个单位长度 | ||
| C. | 向右平移$\frac{π}{12}$个单位长度 | D. | 向左平移$\frac{π}{12}$个单位长度 |
14.已知$α∈(\frac{π}{2},π)$,$sinα=\frac{4}{5}$,则sin2α=( )
| A. | $-\frac{24}{25}$ | B. | $-\frac{7}{25}$ | C. | $\frac{7}{25}$ | D. | $\frac{24}{25}$ |
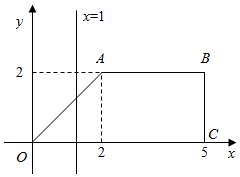 如图,直角梯形OABC位于直线x=t(0≤t≤5)右侧的图形面积为f(t).
如图,直角梯形OABC位于直线x=t(0≤t≤5)右侧的图形面积为f(t).