题目内容
9.已知集合A=$\{x|y=\sqrt{{x^2}-x-6}\}$,集合B=$\{x|x=lo{g_{\frac{1}{2}}}a,a>1\}$,则(∁RA)∩B=( )| A. | {x|-3≤x<0} | B. | {x|-2≤x<0} | C. | {x|-3<x<0} | D. | {x|-2<x<0} |
分析 通过求解一元二次不等式和对数函数的值域分别化简集合A与B,然后直接利用补集及交集运算求解.
解答 解:由A={x|x2-x-6≥0}={x|x≤-2或x≥3},
所以∁RA={x|-2<x<3},
又B=B=$\{x|x=lo{g_{\frac{1}{2}}}a,a>1\}$={x|x<0},
所以(∁RA)∩B={x|-2<x<0},
故选:D.
点评 本题考查了补集及交集运算,考查了函数的定义域,对数函数的值域的解法,是基础的运算题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.已知过点A(0,0)和B(4,m)的直线与直线2x-y-1=0平行,则m的值为( )
| A. | -8 | B. | -2 | C. | 2 | D. | 8 |
17.在平面直角坐标系中,A,B分别是x轴和y轴上的动点,若以AB为直径的圆C与直线3x+y-4=0相切,则圆C面积的最小值为( )
| A. | $\frac{5π}{4}$ | B. | $\frac{2π}{5}$ | C. | $(6-2\sqrt{5})π$ | D. | $\frac{5π}{2}$ |
4.若关于a,b的代数式f(a,b)满足:
①f(a,a)=a
②f(ka,kb)=kf(a,b)
③f(a1+a2,b1+b2)=f(a1,b1)+f(a2,b2)
④f(a,b)=f(b,$\frac{a+b}{2}$)
则f(x,y)=( )
①f(a,a)=a
②f(ka,kb)=kf(a,b)
③f(a1+a2,b1+b2)=f(a1,b1)+f(a2,b2)
④f(a,b)=f(b,$\frac{a+b}{2}$)
则f(x,y)=( )
| A. | $\frac{x-2y}{3}$ | B. | $\frac{2x+y}{3}$ | C. | $\frac{x+2y}{3}$ | D. | $\frac{2x-y}{3}$ |
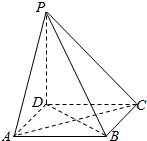 如图,四棱锥P-ABCD的各棱长都为a.
如图,四棱锥P-ABCD的各棱长都为a.