题目内容
设集合A={(x,y)|y=x2+ax+2},B={(x,y)|y=x+1,0≤x≤2},A∩B≠∅,求实数a的取值范围.
考点:集合的包含关系判断及应用
专题:计算题,集合
分析:问题转化为方程y=x2-ax+2与方程y=x+1在0≤x≤2范围内有解.
解答:
解:问题转化为方程y=x2-ax+2与方程y=x+1在0≤x≤2范围内有解.
则:令g(x)=x2-(a+1)x+1=0在0≤x≤2内有根.
所以①0≤
≤2;②g(0)≥0;③g(2)≥0;④△=(a+1)2-4≥0
解上四个不等式得:1≤a≤
.
则:令g(x)=x2-(a+1)x+1=0在0≤x≤2内有根.
所以①0≤
| a+1 |
| 2 |
解上四个不等式得:1≤a≤
| 3 |
| 2 |
点评:本题考查集合的包含关系判断及应用,考查学生分析解决问题的能力,问题转化为方程y=x2-ax+2与方程y=x+1在0≤x≤2范围内有解是关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案
相关题目
 如图,已知几何体的底面ABCD为正方形,AC∩DB=N,PD⊥面ABCD,EC∥PD,PD=CD=2EC=2.
如图,已知几何体的底面ABCD为正方形,AC∩DB=N,PD⊥面ABCD,EC∥PD,PD=CD=2EC=2.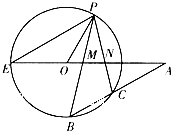 如图,E,P,B,C为圆O上的四点,直线PB,PC,BC分别交直线EO于M,N三点,且PM=PN.
如图,E,P,B,C为圆O上的四点,直线PB,PC,BC分别交直线EO于M,N三点,且PM=PN.