题目内容
6．已知平行四边形三个顶点的坐标分别为A（-3，0），B（2，-2），C（5，2），则第四个顶点D的坐标不可能是（ ）| A． | （10，0） | B． | （0，4） | C． | （-6，-4） | D． | （6，-1） |
分析 利用平行四边形的性质、斜率计算公式即可得出．
解答 解：由已知可得：kAB=kCD，kAC=kBD，kAD=kBC．
kAB=$\frac{-2-0}{2-（-3）}$=-$\frac{2}{5}$，kAC=$\frac{0-2}{-3-5}$=$\frac{1}{4}$，kBC=$\frac{-2-2}{2-5}$=$\frac{4}{3}$．
经过验证可得：不可能为：（6，-1）．
故选：D．
点评 本题考查了平行四边形的性质、斜率计算公式，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
14．若一圆弧长等于它所在圆的内接正三角形的边长，则该弧所对的圆心角弧度数为（ ）
| A． | $\frac{π}{3}$ | B． | $\sqrt{3}$ | C． | $\frac{2π}{3}$ | D． | 2 |
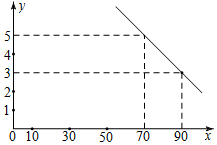近几年，由于环境的污染，雾霾越来越严重，某环保公司销售一种PM2.5颗粒物防护口罩深受市民欢迎．已知这种口罩的进价为40元，经销过程中测出年销售量y（万件）与销售单价x（元）存在如图所示的一次函数关系，每年销售这种口罩的总开支z（万元）（不含进价）与年销量y（万件）存在函数关系z=10y+42.5．
11．定义在实数集R上的函数f（x）都可以写为一个奇函数g（x）与一个偶函数h（x）之和的形式，如果f（x）=2x+1，那么（ ）
| A． | $g（x）=\frac{{{2^x}-{2^{-x}}}}{2}$，$h（x）=\frac{{{2^x}+{2^{-x}}}}{2}$ | B． | $g（x）=\frac{{{2^x}-{2^{-x}}}}{2}$，$h（x）=1+\frac{{{2^x}+{2^{-x}}}}{2}$ | ||
| C． | $g（x）=1+\frac{{{2^x}-{2^{-x}}}}{2}$，$h（x）=\frac{{{2^x}+{2^{-x}}}}{2}$ | D． | $g（x）=\frac{{{2^x}-{2^{-x}}+1}}{2}$，$h（x）=\frac{{{2^x}+{2^{-x}}+1}}{2}$ |