题目内容
已知数列{an}的前n项和Sn=2an+1-1,且a1=2,则S2= ,an= .
考点:数列的求和
专题:等差数列与等比数列
分析:利用赋值法求得a2,进而求得s2,再利用n>1时,Sn-Sn-1=an求得an+1=
an,即可得出结论.
| 3 |
| 2 |
解答:
解:由Sn=2an+1-1可得a1=2a2-1,解得a2=
,S2=2+
=
.
又n>1时,Sn-Sn-1=2an+1-2an,即an+1=
an,
∴an=
(
)n-2=(
)n-1(n>1)
∴an=
.
故答案为:
,an=
.
| 3 |
| 2 |
| 3 |
| 2 |
| 7 |
| 2 |
又n>1时,Sn-Sn-1=2an+1-2an,即an+1=
| 3 |
| 2 |
∴an=
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∴an=
|
故答案为:
| 7 |
| 2 |
|
点评:本题主要考查利用公式n>1时,Sn-Sn-1=an求数列的通项公式的方法,属基础题.

练习册系列答案
相关题目
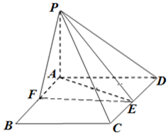 如图,P-AD-C是直二面角,四边形ABCD为菱形,且∠BAD=120°,AB=2,PA⊥AD,E是CD的中点,设PC与平面ABCD所成的角为45°.
如图,P-AD-C是直二面角,四边形ABCD为菱形,且∠BAD=120°,AB=2,PA⊥AD,E是CD的中点,设PC与平面ABCD所成的角为45°.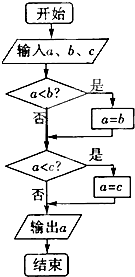 阅读如图的算法流程图:若a=sin60°,b=cos60°,c=tan60°,则输出的应该是
阅读如图的算法流程图:若a=sin60°,b=cos60°,c=tan60°,则输出的应该是