题目内容
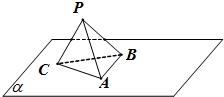已知三棱锥P-ABC的侧面PAC⊥底面ABC，侧棱PA⊥AB，且PA=PC=AC=AB=4．如图AB?平面α，以直线AB为轴旋转三棱锥，记该三棱锥在平面α上的俯视图面积为S，则S的最小值是考点：简单空间图形的三视图
专题：空间位置关系与距离
分析：由侧面PAC⊥底面ABC可得：旋转过程中等边△PAC在底面上的射影总在侧面PAC与平面α的交线l上，且长度范围是[2
，4]，由已知可推证AB⊥l，进而可得S的最值．
| 3 |
解答：
解：取AC的中点D，
由PA=PC=AC，可得PD⊥AC，
又∵侧面PAC⊥底面ABC，侧面PAC∩底面ABC=AC，PD?侧面PAC
∴PD⊥底面ABC，
又∵AB?底面ABC，
∴PD⊥AB，
又∵PA⊥AB，PA∩PD=P，
∴AB⊥平面PAC，
∴旋转过程中等边△PAC在底面上的射影总在侧面PAC与平面α的交线l上，
且长度范围是[2
，4]，
又∵AB⊥l，
所以S最小值为4
，最大值为8．
故答案为：4
，8．
由PA=PC=AC，可得PD⊥AC，
又∵侧面PAC⊥底面ABC，侧面PAC∩底面ABC=AC，PD?侧面PAC
∴PD⊥底面ABC，
又∵AB?底面ABC，
∴PD⊥AB，
又∵PA⊥AB，PA∩PD=P，
∴AB⊥平面PAC，
∴旋转过程中等边△PAC在底面上的射影总在侧面PAC与平面α的交线l上，
且长度范围是[2
| 3 |
又∵AB⊥l，
所以S最小值为4
| 3 |
故答案为：4
| 3 |
点评：本题考查的知识点是简单几何体的三视图，其中分析出等边△PAC在底面上的射影总在侧面PAC与平面α的交线l上，且长度范围是[2
，4]，是解答的关键．
| 3 |
练习册系列答案
相关题目