题目内容
5.根据已知条件求方程:(1)已知椭圆的两个焦点坐标分别是(-1,0),(1,0),并且经过点(1,-$\frac{3}{2}$),求它的标准方程;
(2)求与椭圆$\frac{{x}^{2}}{40}$+$\frac{{y}^{2}}{15}$=1有相同焦点,且离心率e=$\frac{5}{4}$的双曲线的标准方程.
分析 (1)设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),由题意可得c=1,代入点(1,-$\frac{3}{2}$),解方程可得a,b,进而得到所求椭圆方程;
(2)求出椭圆的焦点,可得双曲线的c=5,运用离心率公式可得a=4,进而得到b=3,即可得到双曲线的方程.
解答 解:(1)设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
由题意可得c=1,$\frac{1}{{a}^{2}}$+$\frac{9}{4{b}^{2}}$=1,c2=a2-b2,
解得a=2,b=$\sqrt{3}$,
即有椭圆方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(2)椭圆$\frac{{x}^{2}}{40}$+$\frac{{y}^{2}}{15}$=1的焦点为(±5,0),
即有双曲线的c=5,
设双曲线的方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0),
且a2+b2=25,又e=$\frac{c}{a}$=$\frac{5}{4}$,
解得a=4,b=3,
则双曲线的方程为$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1.
点评 本题考查椭圆和双曲线的方程和性质,考查离心率公式和焦点坐标,考查运算能力,属于基础题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
10.已知函数f(x)=ax-3(a>0且a≠1),f(x0)=0,若x0∈(0,1),则实数a的取值范围是( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,+∞) |
10.阅读如图所示的程序框图,若输入a=$\frac{9}{19}$,则输出的k值是( )
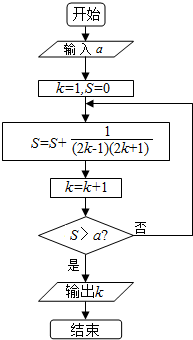

| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
14.已知f(x)是定义在R上的奇函数,且当x∈(0,+∞)时,f(x)=log2x,在f(-8)=( )
| A. | 3 | B. | $\frac{1}{3}$ | C. | -$\frac{1}{3}$ | D. | -3 |