Question

3．在正三棱柱ABC-A₁B₁C₁中，若AB₁⊥BC₁，求证：AB₁⊥A₁C．

Answer 1

分析 连结A₁C，AC₁交点为E，则点E是A₁C的中点．取AB的中点D，连结CD、DE，则DE∥BC₁．求证线线垂直，往往寻求线面垂直，只要证得AB₁⊥平面A₁CD即可

解答 证明：如图所示，连结A₁C，AC₁交点为E，则点E是A₁C的中点．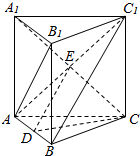

取AB的中点D，连结CD、DE，则DE∥BC₁．
又AB₁⊥BC₁，
∴DE⊥AB₁，
又△ABC是正三角形，
∴CD⊥AB．
又平面ABC⊥平面BB₁A₁A，平面ABC∩平面BB₁A₁A=AB，CD?平面ABC，
∴CD⊥平面BB₁A₁A．
又AB₁?平面BB₁A₁A，
∴AB₁⊥CD．
又CD?平面A₁CD，DE?平面A₁CD，CD∩DE=D，
∴AB₁⊥平面A₁CD．
又A₁C?平面A₁CD，
∴AB₁⊥A₁C．

点评 本题主要考查了线面垂直的性质和判定，同时考查了空间想象能力、运算求解的能力、以及转化与划归的思想，属于中档题