题目内容
7.求下列函数的值域:①f(x)=$\frac{1}{1-x(1-x)}$;
②y=x+$\sqrt{1-2x}$.
分析 ①配方得到$f(x)=\frac{1}{(x-\frac{1}{2})^{2}+\frac{3}{4}}$,这样根据$(x-\frac{1}{2})^{2}+\frac{3}{4}≥\frac{3}{4}$便可求出$\frac{1}{1-x(1-x)}$的范围,即求出该函数的值域;
②可换元得到$\sqrt{1-2x}=t(t≥0)$,可解出x=$\frac{1-{t}^{2}}{2}$,从而得出y=$-\frac{1}{2}(t-1)^{2}+1$,由t≥0便可得出y的范围,即求出该函数的值域.
解答 解:①$f(x)=\frac{1}{{x}^{2}-x+1}=\frac{1}{(x-\frac{1}{2})^{2}+\frac{3}{4}}$;
∵$(x-\frac{1}{2})^{2}+\frac{3}{4}≥\frac{3}{4}$;
∴$0<\frac{1}{(x-\frac{1}{2})^{2}+\frac{3}{4}}≤\frac{4}{3}$;
∴该函数的值域为(0,$\frac{4}{3}$];
②令$\sqrt{1-2x}=t$,(t≥0),∴$x=\frac{1-{t}^{2}}{2}$;
∴$y=\frac{1-{t}^{2}}{2}+t=-\frac{1}{2}(t-1)^{2}+1$;
∵t≥0;
∴$-\frac{1}{2}(t-1)^{2}+1≤1$;
∴该函数的值域为(-∞,1].
点评 考查函数值域的概念,配方法求二次函数的范围,以及根据不等式的性质求函数值域的方法,换元法求函数值域的方法.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
17.若点P(x0,y0)在圆C:x2+y2=r2的内部,则直线xx0+yy0=r2与圆C的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 无法确定 |
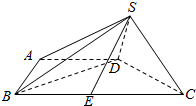 如图,四棱锥S-ABCD中,BC∥AD,BC=2AB=2AD=2,SD=$\frac{1}{2}$,BD⊥SD,∠ABC=60°,E为BC的中点.
如图,四棱锥S-ABCD中,BC∥AD,BC=2AB=2AD=2,SD=$\frac{1}{2}$,BD⊥SD,∠ABC=60°,E为BC的中点.