题目内容
18.设f(x)=$\frac{{e}^{x}-{e}^{-x}}{2}$,g(x)=$\frac{{e}^{x}+{e}^{-x}}{2}$,求证:(1)[g(x)]2-[f(x)]2=1;
(2)f(2x)=2f(x)•g(x);
(3)g(2x)=[g(x)]2+[f(x)]2.
分析 把已知式子整体代要证的等式化简可得.
解答 证明:(1)∵f(x)=$\frac{{e}^{x}-{e}^{-x}}{2}$,g(x)=$\frac{{e}^{x}+{e}^{-x}}{2}$,
∴[g(x)]2-[f(x)]2=[$\frac{{e}^{x}+{e}^{-x}}{2}$]2-[$\frac{{e}^{x}-{e}^{-x}}{2}$]2
=$\frac{{e}^{2x}+{2}^{-2x}+2}{4}$-$\frac{{e}^{2x}+{e}^{-2x}-2}{4}$=$\frac{2-(-2)}{4}$=1;
(2)∵f(x)=$\frac{{e}^{x}-{e}^{-x}}{2}$,g(x)=$\frac{{e}^{x}+{e}^{-x}}{2}$,
∴f(2x)=$\frac{{e}^{2x}-{e}^{-2x}}{2}$=$\frac{({e}^{x}+{e}^{-x})({e}^{x}-{e}^{-x})}{2}$
=2•$\frac{{e}^{x}-{e}^{-x}}{2}$•$\frac{{e}^{x}+{e}^{-x}}{2}$=2f(x)•g(x);
(3))∵f(x)=$\frac{{e}^{x}-{e}^{-x}}{2}$,g(x)=$\frac{{e}^{x}+{e}^{-x}}{2}$,
∴[g(x)]2+[f(x)]2=[$\frac{{e}^{x}+{e}^{-x}}{2}$]2+[$\frac{{e}^{x}-{e}^{-x}}{2}$]2
=$\frac{{e}^{2x}+{2}^{-2x}+2}{4}$+$\frac{{e}^{2x}+{e}^{-2x}-2}{4}$=$\frac{{e}^{2x}+{e}^{-2x}}{2}$=g(2x)
点评 本题考查函数解析式的求解,整体代入是解决问题的关键,属基础题.

 阅读快车系列答案
阅读快车系列答案| A. | [-$\frac{5π}{12}$,0] | B. | [-$\frac{π}{3}$,0] | C. | [0,$\frac{π}{3}$] | D. | [$\frac{π}{6}$,$\frac{π}{2}$] |
| A. | 10($\sqrt{3}$-1) | B. | 10($\sqrt{2}$+1) | C. | 10($\sqrt{2}$-1) | D. | 10($\sqrt{3}$+1) |
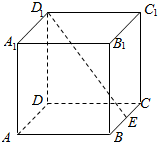 姐图,在正方体ABCD-A1B1C1D1中,E为BC的中点,点P在正方体表面上移动,且满足B1P⊥D1E,则点B1和点P构成的图形是( )
姐图,在正方体ABCD-A1B1C1D1中,E为BC的中点,点P在正方体表面上移动,且满足B1P⊥D1E,则点B1和点P构成的图形是( )| A. | 三角形 | B. | 四边形 | C. | 曲边形 | D. | 五边形 |
| A. | {α|α=k•360°+$\frac{π}{6}$,k∈Z} | B. | {α|α=2kπ+30°,k∈Z} | ||
| C. | {α|α=2k•360°+30°,k∈Z} | D. | {α|α=2kπ+$\frac{π}{6}$,k∈Z} |
 如图,已知点F(1,0),点A,B分别在x轴、y轴上运动,且满足AB⊥BF,$\overrightarrow{AD}$=2$\overrightarrow{AB}$,设点D的轨迹为C.
如图,已知点F(1,0),点A,B分别在x轴、y轴上运动,且满足AB⊥BF,$\overrightarrow{AD}$=2$\overrightarrow{AB}$,设点D的轨迹为C.