题目内容
15．若0＜x＜$\frac{3}{5}$，则x（3-5x）的最大值是$\frac{9}{20}$．分析 利用x（3-5x）=$\frac{1}{5}$[5x（3-5x）]≤$\frac{1}{5}$•$（\frac{5x+3-5x}{2}）^{2}$=$\frac{9}{20}$，即可得出结论．
解答 解：∵0＜x＜$\frac{3}{5}$，∴3-5x＞0，
∴x（3-5x）=$\frac{1}{5}$[5x（3-5x）]≤$\frac{1}{5}$•$（\frac{5x+3-5x}{2}）^{2}$=$\frac{9}{20}$，
当且仅当5x=3-5x，即x=$\frac{3}{10}$时取等号，
∴x（3-5x）的最大值是$\frac{9}{20}$．
故答案为：$\frac{9}{20}$．
点评 本题考查二次函数的最大值，考查基本不等式的运用，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
6．
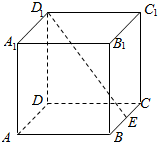姐图，在正方体ABCD-A1B1C1D1中，E为BC的中点，点P在正方体表面上移动，且满足B1P⊥D1E，则点B1和点P构成的图形是（ ）
姐图，在正方体ABCD-A1B1C1D1中，E为BC的中点，点P在正方体表面上移动，且满足B1P⊥D1E，则点B1和点P构成的图形是（ ）| A． | 三角形 | B． | 四边形 | C． | 曲边形 | D． | 五边形 |
如图，已知点F（1，0），点A，B分别在x轴、y轴上运动，且满足AB⊥BF，$\overrightarrow{AD}$=2$\overrightarrow{AB}$，设点D的轨迹为C．
如图所示，一条边利用足够长的墙，用12m长的篱笆围出一块五边形的苗圃．已知EA⊥AB，CB⊥AB，∠C=∠D=∠E，设CD=DE=x（m），五边形的面积为S．