题目内容
16．设P表示平面内的动点，属于下列集合的点组成什么图形？（1）{P|PA=PB}（A，B是两个定点）；
（2）{P|PO=3cm}（O是定点）．
分析 （1）由已知可得：即P到A，B的距离相等，故P在线段AB的垂直平分线上；
（2）由已知可得：P到定点O的距离为定值3，故P表示以O为圆心以3为半径的圆．
解答 解：（1）∵{P|PA=PB}，
即P到A，B的距离相等，
故P在线段AB的垂直平分线上，
故点P构成一条直线；
（2）∵{P|PO=3}．
即P到定点O的距离为定值3，
故P表示以O为圆心以3为半径的圆，
故P表示一个圆．
点评 本题考查的知识点是性质描述法表示一个集合，正确理解垂直平分线和圆的定义，是解答的关键．
练习册系列答案
名校课堂系列答案
相关题目
6．
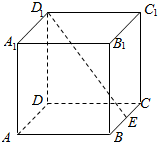姐图，在正方体ABCD-A1B1C1D1中，E为BC的中点，点P在正方体表面上移动，且满足B1P⊥D1E，则点B1和点P构成的图形是（ ）
姐图，在正方体ABCD-A1B1C1D1中，E为BC的中点，点P在正方体表面上移动，且满足B1P⊥D1E，则点B1和点P构成的图形是（ ）| A． | 三角形 | B． | 四边形 | C． | 曲边形 | D． | 五边形 |
1．已知AD是△ABC的角平分线，且△ABD的面积与△ACD的面积比为3：2．
（1）求$\frac{sinB}{sinC}$的值；
（2）若AD=3$\sqrt{2}$，∠C=2∠B，求△ABC的面积．
（1）求$\frac{sinB}{sinC}$的值；
（2）若AD=3$\sqrt{2}$，∠C=2∠B，求△ABC的面积．
8．与30°角终边相同的角的集合是（ ）
| A． | {α|α=k•360°+$\frac{π}{6}$，k∈Z} | B． | {α|α=2kπ+30°，k∈Z} | ||
| C． | {α|α=2k•360°+30°，k∈Z} | D． | {α|α=2kπ+$\frac{π}{6}$，k∈Z} |
如图所示，一条边利用足够长的墙，用12m长的篱笆围出一块五边形的苗圃．已知EA⊥AB，CB⊥AB，∠C=∠D=∠E，设CD=DE=x（m），五边形的面积为S．