题目内容
4.已知过点A(0,1)且斜率为k的直线l与圆C:(x-2)2+(y-3)2=1交于M,N两点.(1)求k的取值范围;
(2)若S△MON=6tan∠MON,其中O为坐标原点,求|MN|.
分析 (1)设出直线方程,利用直线与圆的位置关系,列出不等式求解即可.
(2)设出M,N的坐标,利用直线与圆的方程联立,通过韦达定理,结合已知条件,转化为向量的数量积,求出直线的斜率,然后判断直线与圆的位置关系求解|MN|即可.
解答 解:(1)由题设,可知直线l的方程为y=kx+1,因为直线l与圆C交于两点,
所以$\frac{|2k-3+1|}{\sqrt{1+{k}^{2}}}$<1.解得$\frac{4-\sqrt{7}}{3}$<k<$\frac{4+\sqrt{7}}{3}$.
所以k的取值范围为:($\frac{4-\sqrt{7}}{3}$,$\frac{4+\sqrt{7}}{3}$).
(2)设M(x1,y1),N(x2,y2).将y=kx+1代入方程:(x-2)2+(y-3)2=1,
整理得(1+k2)x2-4(1+k)x+7=0.所以x1+x2=$\frac{4(1+k)}{1+{k}^{2}}$,x1x2=$\frac{7}{1+{k}^{2}}$,
$\overrightarrow{OM}•\overrightarrow{ON}$=x1x2+y1y2=(1+k)2(x1x2)+k(x1+x2)+1=$\frac{4k(1+k)}{1+{k}^{2}}+8$.
由题设可得S△MON=6tan∠MON,可得$\overrightarrow{OM}•\overrightarrow{ON}$=12.
即$\frac{4k(1+k)}{1+{k}^{2}}+8$=12,解得k=1,所以直线l的方程为y=x+1.
故圆心C在直线l上,所以|MN|=2.
点评 本题考查直线与圆的位置关系的综合应用,圆的方程的应用,考查转化思想以及计算能力.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
15.某市组织500名志愿者参加敬老活动,为方便安排任务将所有志愿者按年龄(单位:岁)分组,得到的频率分布表如下.现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人担任联系人.
(1)应分别在第1,2,3组中抽取志愿者多少人?
(2)从这6人中随机抽取2人担任本次活动的宣传员,求至少有1人年龄在第3组的概率.
| 年龄(岁) | 频率 | |
| 第1组 | [25,30) | 0.1 |
| 第2组 | [30,35) | 0.1 |
| 第3组 | [35,40) | 0.4 |
| 第4组 | [40,45) | 0.3 |
| 第5组 | [45,50] | 0.1 |
(2)从这6人中随机抽取2人担任本次活动的宣传员,求至少有1人年龄在第3组的概率.
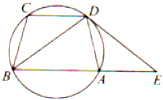 如图,已知圆上的四点A、B、C、D,CD∥AB,过点D的圆的切线DE与BA的延长线交于E点.
如图,已知圆上的四点A、B、C、D,CD∥AB,过点D的圆的切线DE与BA的延长线交于E点.