题目内容
7.已知数列{an}中a1,a2的分别是直线2x+y-2=0的横、纵截距,且$\frac{{{a_{n+1}}-{a_{n-1}}}}{{{a_n}+{a_{n+1}}}}$=2(n≥2,n∈N*),则数列{an}的通项公式为an=(3n-4)(-1)n.分析 数列{an}中a1,a2的分别是直线2x+y-2=0的横、纵截距,可得a1=1,a2=2.$\frac{{{a_{n+1}}-{a_{n-1}}}}{{{a_n}+{a_{n+1}}}}$=2(n≥2,n∈N*),化为:an+1+an=-(an+an-1),利用等比数列的通项公式可得:an+1+an=3×(-1)n-1.变形为:$\frac{{a}_{n+1}}{(-1)^{n+1}}$-$\frac{{a}_{n}}{(-1)^{n}}$=3,再利用等差数列的通项公式即可得出.
解答 解:数列{an}中a1,a2的分别是直线2x+y-2=0的横、纵截距,∴a1=1,a2=2.
∵$\frac{{{a_{n+1}}-{a_{n-1}}}}{{{a_n}+{a_{n+1}}}}$=2(n≥2,n∈N*),化为:an+1+an=-(an+an-1),
∴数列{an+1+an}是等比数列,首项为3,公比为-1.
∴an+1+an=3×(-1)n-1.
变形为:$\frac{{a}_{n+1}}{(-1)^{n+1}}$-$\frac{{a}_{n}}{(-1)^{n}}$=3,
∴数列$\{\frac{{a}_{n}}{(-1)^{n}}\}$是等差数列,公差为3,首项为-1.
∴$\frac{{a}_{n}}{(-1)^{n}}$=-1+3(n-1)=3n-4.
∴an=(3n-4)(-1)n.
故答案为:an=(3n-4)(-1)n.
点评 本题考查了递推关系、等差数列与等比数列的通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
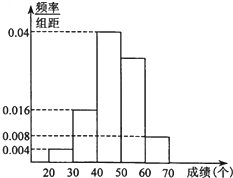 体育课上,李老师对初三(1)班50名学生进行跳绳测试.现测得他们的成绩(单位:个)全部介于20到70之间,将这些成绩数据进行分组(第一组:(20,30],第二组:(30,40],…,第五组:(60,70]),并绘制成如图所示的频率分布直方图.
体育课上,李老师对初三(1)班50名学生进行跳绳测试.现测得他们的成绩(单位:个)全部介于20到70之间,将这些成绩数据进行分组(第一组:(20,30],第二组:(30,40],…,第五组:(60,70]),并绘制成如图所示的频率分布直方图.