题目内容
2.为降低雾霾等恶劣气候对居民的影响,某公司研发了一种新型防雾霾产品.每一台新产品在进入市场前都必须进行两种不同的检测,只有两种检测都合格才能进行销售,否则不能销售.已知该新型防雾霾产品第一种检测不合格的概率为$\frac{1}{6}$,第二种检测不合格的概率为$\frac{1}{10}$,两种检测是否合格相互独立.(Ⅰ)求每台新型防雾霾产品不能销售的概率;
(Ⅱ)如果产品可以销售,则每台产品可获利40元;如果产品不能销售,则每台产品亏损80元(即获利-80元).现有该新型防雾霾产品3台,随机变量X表示这3台产品的获利,求X的分布列及数学期望.
分析 (Ⅰ)(Ⅰ)记“每台新型防雾霾产品不能销售”为事件A,由此利用对立事件概率计算公式能求出每台新型防雾霾产品不能销售的概率.
(Ⅱ)由已知,可知X的取值为-240,-120,0,120.分别求出相应的概率,由此能求出X的分布列及EX.
解答 解:(Ⅰ)(Ⅰ)记“每台新型防雾霾产品不能销售”为事件A,
则P(A)=1-(1-$\frac{1}{6}$)(1-$\frac{1}{10}$)=$\frac{1}{4}$.
所以,该产品不能销售的概率为$\frac{1}{4}$.
(Ⅱ)由已知,可知X的取值为-240,-120,0,120.
P(X=-240)=($\frac{1}{4}$)3=$\frac{1}{64}$,
P(X=-120)=${C}_{3}^{2}(\frac{1}{4})^{2}(\frac{3}{4})$=$\frac{9}{64}$,
P(X=0)=${C}_{3}^{1}(\frac{1}{4})(\frac{3}{4})^{2}$=$\frac{27}{64}$,
P(X=120)=($\frac{3}{4}$)3=$\frac{27}{64}$,
∴X的分布列为:
| X | -240 | -120 | 0 | 120 |
| P | $\frac{1}{64}$ | $\frac{9}{64}$ | $\frac{27}{64}$ | $\frac{27}{64}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列及数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
相关题目
11.在等比数列{an}中,若a1,a2,…,a8都是正数,且公比q≠1,则( )
| A. | a1+a8>a4+a5 | B. | a1+a8<a4+a5 | ||
| C. | a1+a8=a4+a5 | D. | a1+a8与a4+a5的大小关系不定 |

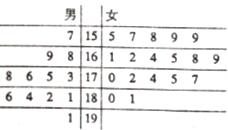 某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试跳远的成绩用茎叶图表示如下(单位:cm):
某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试跳远的成绩用茎叶图表示如下(单位:cm):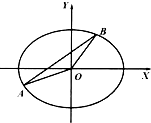 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,不经过原点O的直线l:y=kx+m(k>0)与椭圆E相交于不同的两点A、B,直线OA,AB,OB的斜率依次构成等比数列.
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,不经过原点O的直线l:y=kx+m(k>0)与椭圆E相交于不同的两点A、B,直线OA,AB,OB的斜率依次构成等比数列. 如图,AB为圆O的直径,PA垂直圆O所在的平面,点C为圆O上的一点.
如图,AB为圆O的直径,PA垂直圆O所在的平面,点C为圆O上的一点.