题目内容
17.已知A(2,1),O(0,0),点M(x,y)满足$\left\{\begin{array}{l}{1≤x≤2}\\{y≤2}\\{2x-y≤2}\end{array}\right.$,则Z=$\overrightarrow{OA}$•$\overrightarrow{AM}$的最大值为1.分析 画出满足条件的平面区域,求出角点的坐标,求出z的表达式,结合图象求出z的最大值即可.
解答 解:画出满足条件的平面区域,如图示: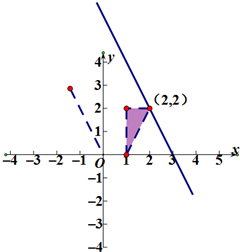 ,
,
由$\left\{\begin{array}{l}{y=2}\\{2x-y=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$,
由Z=$\overrightarrow{OA}$•$\overrightarrow{AM}$=2x+y-5,得:y=-2x+z-5,
平移直线y=-2x,
显然直线过(2,2)时,z最大,
z的最大值是1,
故答案为:1.
点评 本题考查了简单的线性规划问题,考查数形结合思想,是一道中档题.

练习册系列答案
相关题目
8.若复数z满足z(1+i)=2-2i(i为虚数单位),则|z|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
9.甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取5次,记录如下:
(Ⅰ)用茎叶图表示这两组数据;
(Ⅱ)现要从中选派一人参加数学竞赛,你认为选派哪位学生参加合适?请说明理由.(用样本数据特征来说明.)
| 甲 | 88 | 89 | 92 | 90 | 91 |
| 乙 | 84 | 88 | 96 | 89 | 93 |
(Ⅱ)现要从中选派一人参加数学竞赛,你认为选派哪位学生参加合适?请说明理由.(用样本数据特征来说明.)
 如图,AB为圆O的直径,PA垂直圆O所在的平面,点C为圆O上的一点.
如图,AB为圆O的直径,PA垂直圆O所在的平面,点C为圆O上的一点.