题目内容
15.已知a>b>0,试指出$\frac{a+b}{2}$-$\sqrt{ab}$,$\frac{(a-b)^{2}}{8a}$,$\frac{(a-b)^{2}}{8b}$的大小关系,并给出证明.分析 由不等式的性质可得$\frac{(a-b)^{2}}{8a}<\frac{(a-b)^{2}}{8b}$,由$\frac{a+b}{2}-\sqrt{ab}=\frac{(\sqrt{a}-\sqrt{b})^{2}}{2}$,然后利用作商法比较$\frac{a+b}{2}$-$\sqrt{ab}$与$\frac{(a-b)^{2}}{8a}$,$\frac{(a-b)^{2}}{8b}$的大小得答案.
解答 解:$\frac{(a-b)^{2}}{8a}$<$\frac{a+b}{2}$-$\sqrt{ab}$<$\frac{(a-b)^{2}}{8b}$.
事实上,
∵a>b>0,
∴$\frac{1}{b}>\frac{1}{a}>0$,
又(a-b)2>0,
∴$\frac{(a-b)^{2}}{8a}<\frac{(a-b)^{2}}{8b}$;
∵$\frac{a+b}{2}-\sqrt{ab}=\frac{(\sqrt{a}-\sqrt{b})^{2}}{2}$,
且$\frac{\frac{(\sqrt{a}-\sqrt{b})^{2}}{2}}{\frac{(a-b)^{2}}{8a}}=\frac{4a}{(\sqrt{a}+\sqrt{b})^{2}}>\frac{4a}{(2\sqrt{a})^{2}}=1$,
$\frac{\frac{(\sqrt{a}-\sqrt{b})^{2}}{2}}{\frac{(a-b)^{2}}{8b}}=\frac{4b}{(\sqrt{a}+\sqrt{b})^{2}}<\frac{4b}{(2\sqrt{b})^{2}}=1$,
∴$\frac{(a-b)^{2}}{8a}$<$\frac{a+b}{2}$-$\sqrt{ab}$<$\frac{(a-b)^{2}}{8b}$.
点评 本题考查不等式的大小比较,考查了作商法,是中档题.

 53天天练系列答案
53天天练系列答案| A. | 3,(-3,2) | B. | 3,(-5,4) | C. | 9,(-5,4) | D. | 9,(-3,2) |
A规格 | B规格 | C规格 | |
| 第一种钢板 | 2 | 1 | 1 |
| 第二种钢板 | 1 | 3 | 1 |
(1)设需裁第一种钢板x张,第二种钢板y张,用x,y列出符合题意的数学关系式,并在给出的平面直角坐标系中画出相应的平面区域;
(2)在满足需求的条件下,问各裁这两种钢板多少张,所用钢板面积最小?
| A. | 1+3i | B. | 1-3i | C. | 3+i | D. | 3-i |
 正方体ABCD-A1B1C1D1中,点E在棱CC1上,CE=2EC1,AB=6,M,N分别为棱AB和AD的中点.
正方体ABCD-A1B1C1D1中,点E在棱CC1上,CE=2EC1,AB=6,M,N分别为棱AB和AD的中点.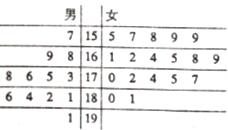 某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试跳远的成绩用茎叶图表示如下(单位:cm):
某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试跳远的成绩用茎叶图表示如下(单位:cm):