题目内容
过原点O的直线MN与双曲线C：
-
=1交于M、N两点，P是双曲线C上异于M、N的点，若直线PM，PN的斜率之积kPM•kPN=
，则双曲线C的离心率e=（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
| D、2 |
考点：双曲线的简单性质
专题：计算题,平面向量及应用,直线与圆,圆锥曲线的定义、性质与方程
分析：设M（m，n），N（-m，-n），P（x，y），运用直线的斜率公式以及点在双曲线则满足双曲线方程，两式相减，即可得到a，b的关系式，再由离心率公式计算即可得到．
解答：
解：设M（m，n），N（-m，-n），P（x，y），
则kPM=
，kPN=
，
则有kPM•kPN=
=
，
由于
-
=1，
-
=1．
两式相减可得
=
，
即有
=
=
，
则e2=
=
=1+
=
，
则e=
．
故选A．
则kPM=
| y-n |
| x-m |
| y+n |
| x+m |
则有kPM•kPN=
| y2-n2 |
| x2-m2 |
| 5 |
| 4 |
由于
| m2 |
| a2 |
| n2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
两式相减可得
| x2-m2 |
| a2 |
| y2-n2 |
| b2 |
即有
| y2-n2 |
| x2-m2 |
| b2 |
| a2 |
| 5 |
| 4 |
则e2=
| c2 |
| a2 |
| a2+b2 |
| a2 |
| 5 |
| 4 |
| 9 |
| 4 |
则e=
| 3 |
| 2 |
故选A．
点评：本题考查双曲线的方程和性质，考查直线的斜率公式的运用，考查点差法的运用，考查离心率的求法，属于中档题．
练习册系列答案
相关题目
已知函数f（x）=ax3-bx-3，若f（-1）=7，则f（1）=（ ）
| A、-7 | B、7 | C、-13 | D、13 |
设集合A={x|-4＜x＜3}，B={x|x≤2}，则A∪B=（ ）
| A、（-4，3） |
| B、（-4，2] |
| C、（-∞，2] |
| D、（-∞，3） |
在平面直角坐标系xOy中，若双曲线：
-
=1（a＞0，b＞0）的两条渐近线与直线l：
-
=1（其中c为双曲线的半焦距）分别交于A、B两点，已知线段AB中点的横坐标为-c，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| x |
| c |
| y |
| b |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
如果直线l⊥平面α，①若直线m⊥l，则m∥α；②若m⊥α，则m∥l；③若m∥α，则m⊥l；④若m∥l，则m⊥α，上述判断正确的是 （ ）
| A、①②③ | B、②③④ |
| C、①③④ | D、②④ |
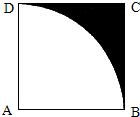如图，在边长为1的正方形ABCD中，以A为圆心，AB为半径作扇形ABD，在该正方形内随机取一点，则此点取自阴影部分的概率是