题目内容
在极坐标系中,点P(2,-
)到直线l:ρsin(θ-
)=1的距离是 .
| π |
| 3 |
| π |
| 6 |
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:由极坐标化为直角坐标,再利用点到直线的距离公式即可得出.
解答:
解:点P(2,-
)化为P(2cos(-
),2sin(-
)),即P(1,-
).
直线l:ρsin(θ-
)=1化为:
ρsinθ-
ρcosθ=1,x-
y+2=0.
∴点P(2,-
)到直线l:ρsin(θ-
)=1的距离=
=3.
故答案为:3.
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 3 |
直线l:ρsin(θ-
| π |
| 6 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
∴点P(2,-
| π |
| 3 |
| π |
| 6 |
| |1+3+2| | ||||
|
故答案为:3.
点评:本题考查了极坐标化为直角坐标、点到直线的距离公式,属于基础题.

练习册系列答案
相关题目
在平面直角坐标系xOy中,若双曲线:
-
=1(a>0,b>0)的两条渐近线与直线l:
-
=1(其中c为双曲线的半焦距)分别交于A、B两点,已知线段AB中点的横坐标为-c,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| x |
| c |
| y |
| b |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
已知a>0,b>0,则下列不等式中不恒成立的是( )
A、
| ||||||
B、(a+b)(
| ||||||
C、
| ||||||
| D、a2+b2+1≥2a+2b |
以下有关线性回归分析的说法不正确的是( )
A、在回归线方程
| ||||
B、用最二乘法求回归直线方程,是寻求使
| ||||
| C、相关系数为r,若r2越接近1,则表明回归线的效果越好 | ||||
| D、相关系数r越小,表明两个变量相关性越弱 |
若a>b>0,c>d>0,则一定有( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
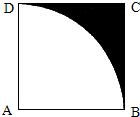 如图,在边长为1的正方形ABCD中,以A为圆心,AB为半径作扇形ABD,在该正方形内随机取一点,则此点取自阴影部分的概率是
如图,在边长为1的正方形ABCD中,以A为圆心,AB为半径作扇形ABD,在该正方形内随机取一点,则此点取自阴影部分的概率是
