题目内容
下列不等式不成立的是（ ）
| A、a2+b2+c2≥ab+bc+ca | ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
考点：不等式的基本性质
专题：不等式的解法及应用
分析：A．利用（a-b）2+（b-c）2+（a-c）2≥0，展开即可得出；
B．平方作差(
+
)2-(
)2，展开即可得出；
C．利用分子有理化
-
=
，
-
=
，即可比较出大小．
D．平方作差(
+
)2-(2
)2，展开即可得出．
B．平方作差(
| a |
| b |
| a+b |
C．利用分子有理化
| a |
| a-1 |
| 1 | ||||
|
| a-2 |
| a-3 |
| 1 | ||||
|
D．平方作差(
| 2 |
| 10 |
| 6 |
解答：
解：A．∵（a-b）2+（b-c）2+（a-c）2≥0，∴a2+b2+c2≥ab+bc+ca，正确；
B．∵(
+
)2-(
)2=2
＞0，∴
+
＞
，因此正确；
C．∵a≥3，
-
=
＜
=
-
，∴
-
＜
-
，因此正确．
D.(
+
)2-(2
)2=4
-12＜0，∴
+
＜2
，因此不正确．
故选：D．
B．∵(
| a |
| b |
| a+b |
| ab |
| a |
| b |
| a+b |
C．∵a≥3，
| a |
| a-1 |
| 1 | ||||
|
| 1 | ||||
|
| a-2 |
| a-3 |
| a |
| a-1 |
| a-2 |
| a-3 |
D.(
| 2 |
| 10 |
| 6 |
| 5 |
| 2 |
| 10 |
| 6 |
故选：D．
点评：本题考查了平方作差、乘法公式、有理化因式比较两个数的大小，考查了计算能力，属于基础题．
练习册系列答案
相关题目
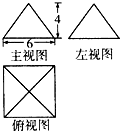
若几何体的三视图如图所示，则该几何体的体积为（ ）
A、
| ||
B、
| ||
C、
| ||
| D、π |
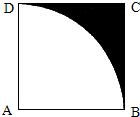如图，在边长为1的正方形ABCD中，以A为圆心，AB为半径作扇形ABD，在该正方形内随机取一点，则此点取自阴影部分的概率是在△ABC中，∠A，∠B，∠C的对边分别为a，b，c，若a=1，且2cosC+c=2b，则△ABC的周长的取值范围是（ ）
| A、[0，2） |
| B、（2，3） |
| C、[2，3） |
| D、（2，3] |