题目内容
13.求点P(m,n)关于直线x+y+b=0对称的点的坐标.分析 设出对称点的坐标列出方程组求解即可.
解答 解:点P(m,n)关于直线x+y+b=0对称的点为(x,y).
可得:$\left\{\begin{array}{l}\frac{n-y}{m-x}=1\\ \frac{x+m}{2}+\frac{y+n}{2}+b=0\end{array}\right.$,即:$\left\{\begin{array}{l}x-y+n-m=0\\ x+y+m+n+2b=0\end{array}\right.$
解得:$\left\{\begin{array}{l}x=-n-b\\ y=-m-b\end{array}\right.$,
点P(m,n)关于直线x+y+b=0对称的点的坐标:(-n-b,-m-b).
点评 本题考查了点关于直线的对称点的求法,对称知识的应用,考查计算能力.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
4.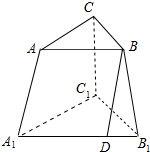 在三棱台A1B1C1-ABC中,点D在A1B1上,且AA1∥BD,点M是△A1B1C1内(含边界)的一个动点,且有平面BDM∥平面A1C,则动点M的轨迹是( )
在三棱台A1B1C1-ABC中,点D在A1B1上,且AA1∥BD,点M是△A1B1C1内(含边界)的一个动点,且有平面BDM∥平面A1C,则动点M的轨迹是( )
 在三棱台A1B1C1-ABC中,点D在A1B1上,且AA1∥BD,点M是△A1B1C1内(含边界)的一个动点,且有平面BDM∥平面A1C,则动点M的轨迹是( )
在三棱台A1B1C1-ABC中,点D在A1B1上,且AA1∥BD,点M是△A1B1C1内(含边界)的一个动点,且有平面BDM∥平面A1C,则动点M的轨迹是( )| A. | 平面 | B. | 直线 | ||
| C. | 线段,但只含1个端点 | D. | 圆 |
1.已知实数a,b,c,d满足$\frac{2+5alna}{2{a}^{2}-ab}$=$\frac{{c}^{2}-mc}{d-4}$=1,在直角坐标系中,点(a,b)和(c,d)的轨迹方程分别为y=f(x),y=g(x),若?x1∈(0,1),?x2∈[1,2],郡有f(x1)≥g(x2)成立,则实数m的最小值为( )
| A. | $\frac{11-5ln2}{2}$ | B. | 2 | C. | 8-5ln2 | D. | 7-5ln2 |
18.设三棱锥的三条侧棱两两互相垂直,且长度分别为2,2$\sqrt{3}$,4,则其外接球的表面积为( )
| A. | 48π | B. | 32π | C. | 20π | D. | 12π |
2.函数f(x)=sin(x+$\frac{π}{6}$)+cos(x+$\frac{π}{6}$)的值域是( )
| A. | [-2,2] | B. | [-1,1] | C. | [-$\sqrt{2}$,$\sqrt{2}$] | D. | [-$\frac{1}{2}$,$\frac{1}{2}$] |
12.设集合M={x|-2<x<3},P={x|x≤-1},那么“x∈M或x∈P”是“x∈M∩P”的( )
| A. | . 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | .充要条件 | D. | . 既不充分也不必要条件 |