题目内容
3.随着社会的发展,汽车正逐步成为人们的代步工具,超速造成的交通事故正逐年上升,交警在处理交通事故的时候多利用刹车痕迹的长度来判断车辆是否超速.已知某种汽车的刹车距离S(米)和汽车车速v(千米/小时)有如下关系:$S=av+\frac{1}{180}{v^2}$,若该种汽车的速度为30千米/小时,则刹车距离为6.5米.在一条限速80千米/小时的道路上发生了一起交通事故,交警测得该种车的刹车距离大于49.5米.(Ⅰ)当汽车时速为60千米/小时,其刹车距离为多少?
(Ⅱ)该车在道路上是否超速行驶?
分析 (Ⅰ)利用汽车的速度为30千米/小时,则刹车距离为6.5米.求出函数的解析式,然后当汽车时速为60千米/小时,代入求解可得其刹车距离.
(Ⅱ)利用函数的解析式,代入刹车距离大于49.5米,然后该车在道路上行驶速度即可.
解答 解:(Ⅰ)$S=av+\frac{1}{180}{v^2}$,若该种汽车的速度为30千米/小时,则刹车距离为6.5米.
可得6.5=30a+$\frac{1}{180}×{30}^{2}$,
解得a=$\frac{1}{20}$,
$S=\frac{1}{20}v+\frac{1}{180}{v}^{2}$,
汽车时速为60千米/小时,其刹车距离为:$S=\frac{1}{20}×60+\frac{1}{180}×{60}^{2}$=23米.
(Ⅱ)交警测得该种车的刹车距离大于49.5米,由$S=\frac{1}{20}v+\frac{1}{180}{v}^{2}$,
可得$\frac{1}{20}v+\frac{1}{180}{v}^{2}>49.5$,v2+9v-8910>0,
解得v>$\frac{-9+\sqrt{81+35640}}{2}$=$\frac{-9+189}{2}$=90.
该车的速度超过90千米/小时,超速行驶.
点评 本题考查函数的解析式的应用,不等式的解法,考查分析问题解决问题的能力.

练习册系列答案
相关题目
13.下列函数中,既是偶函数又在(0,+∞)上是增函数的是( )
| A. | $y={x^{\frac{2}{3}}}$ | B. | $y={x^{\frac{3}{2}}}$ | C. | y=x-2 | D. | $y={x^{-\frac{1}{2}}}$ |
18.在三角形ABC中,A=120°,AB=4,$BC=2\sqrt{19}$,则$\frac{sinB}{sinC}$的值为( )
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{{\sqrt{19}}}{2}$ | D. | $\frac{{2\sqrt{19}}}{19}$ |
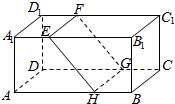 如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4,点H,G分别在AB,CD上,AH=DG=10.
如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4,点H,G分别在AB,CD上,AH=DG=10.