题目内容
2.函数f(x)=sin(x+$\frac{π}{6}$)+cos(x+$\frac{π}{6}$)的值域是( )| A. | [-2,2] | B. | [-1,1] | C. | [-$\sqrt{2}$,$\sqrt{2}$] | D. | [-$\frac{1}{2}$,$\frac{1}{2}$] |
分析 由条件利用两角和差的三角公式,辅助角公式化简函数的解析式,再利用正弦函数的值域求得f(x)的值域.
解答 解:函数f(x)=sin(x+$\frac{π}{6}$)+cos(x+$\frac{π}{6}$)=sinx•$\frac{\sqrt{3}}{2}$+cosx•$\frac{1}{2}$+cosx•$\frac{\sqrt{3}}{2}$-sinx•$\frac{1}{2}$
=$\frac{\sqrt{3}-1}{2}$sinx+$\frac{\sqrt{3}+1}{2}$cosx=$\sqrt{2}$•(sinx$\frac{\sqrt{6}-\sqrt{2}}{4}$+$\frac{\sqrt{6}+\sqrt{2}}{4}$cosx)=sin(x+θ),
其中,cosθ=$\frac{\sqrt{6}-\sqrt{2}}{4}$,sinθ=$\frac{\sqrt{6}+\sqrt{2}}{4}$,
故函数的值域为[-$\sqrt{2}$,$\sqrt{2}$],
故选:C.
点评 本题主要考查两角和差的三角公式,辅助角公式的应用,正弦函数的值域,属于基础题.

练习册系列答案
相关题目
1.已知集合A={-1,0,1,2,3},B={x|(x+1)(x-3)<0},则A∩B=( )
| A. | {-1,3} | B. | {0,1} | C. | {0,1,2} | D. | {1,2,3} |
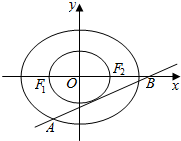 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(0,$\sqrt{3}$),离心率为$\frac{1}{2}$,左右焦点分别为F1(-c,0),F2(c,0).
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(0,$\sqrt{3}$),离心率为$\frac{1}{2}$,左右焦点分别为F1(-c,0),F2(c,0).