题目内容
已知极点为直角坐标系的原点,极轴为x轴正半轴且单位长度相同的极坐标系中,直线l:ρcos(θ-
)=
与直角坐标系中的曲线C:
(θ为参数),交于A、B两点.
(Ⅰ)求直线l在直角坐标系下的方程;
(Ⅱ)求点M(-1,2)与A、B两点的距离之积|MA||MB|.
| π |
| 4 |
| ||
| 2 |
|
(Ⅰ)求直线l在直角坐标系下的方程;
(Ⅱ)求点M(-1,2)与A、B两点的距离之积|MA||MB|.
考点:参数方程化成普通方程
专题:选作题,坐标系和参数方程
分析:(Ⅰ)利用直角坐标与极坐标间的关系,可求直线l在直角坐标系下的方程;
(Ⅱ)求出曲线C的普通方程,与直线方程联立,求出A,B的坐标,即可求点M(-1,2)与A、B两点的距离之积|MA||MB|.
(Ⅱ)求出曲线C的普通方程,与直线方程联立,求出A,B的坐标,即可求点M(-1,2)与A、B两点的距离之积|MA||MB|.
解答:
解:(Ⅰ)由l:ρcos(θ-
)=
得 ρcosθ+ρsinθ=1(3分)
从而l在直角坐标系中方程为x+y=1(4分)
(Ⅱ)曲线C的普通方程为
+x2=1(5分)
由
得
或
从而 A(1,0),B( -
,
).(7分)
又M(-1,2)
所以|MA||MB|=
=
(10分)
| π |
| 4 |
| ||
| 2 |
从而l在直角坐标系中方程为x+y=1(4分)
(Ⅱ)曲线C的普通方程为
| y2 |
| 2 |
由
|
|
|
从而 A(1,0),B( -
| 1 |
| 3 |
| 4 |
| 3 |
又M(-1,2)
所以|MA||MB|=
| (1+1)2+(0-2)2 |
(-
|
| 8 |
| 3 |
点评:本小题主要考查圆的参数方程和直线的极坐标方程与直角坐标方程的互化,以及直线与圆的位置关系,属于基础题.

练习册系列答案
相关题目
已知函数f(x)=-2cosx,x∈[0,π]在点P处的切线与函数g(x)=
x2+lnx在点Q处的切线平行,则直线PQ的斜率为( )
| 1 |
| 2 |
A、
| ||
B、
| ||
| C、2 | ||
| D、π-2 |
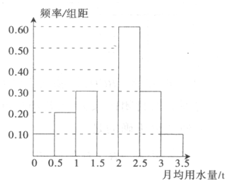 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准?用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图,
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准?用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图,
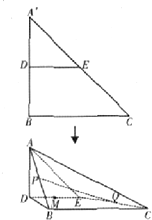 如图,在Rt△A′BC中,A′B=BC=2,D,E分别是A′B,A′C的中点,将△A′DE沿线段DE折起到△ADE,使平面ADE⊥平面DBCE.
如图,在Rt△A′BC中,A′B=BC=2,D,E分别是A′B,A′C的中点,将△A′DE沿线段DE折起到△ADE,使平面ADE⊥平面DBCE.