题目内容
已知a,b,c都是正数,求
+
+
的最小值.
| a |
| b+c |
| b |
| c+a |
| c |
| a+b |
考点:不等式的证明
专题:选作题,不等式
分析:
+
+
+3=(a+b+c)(
+
+
),再利用柯西不等式,即可得出结论.
| a |
| b+c |
| b |
| c+a |
| c |
| a+b |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
解答:
解:
+
+
+3=(a+b+c)(
+
+
)
=
[(b+c)+(c+a)+(a+b)]((
+
+
)≥
(1+1+1)2=
∴
+
+
≥
.
∴
+
+
的最小值为
.
| a |
| b+c |
| b |
| c+a |
| c |
| a+b |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
=
| 1 |
| 2 |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
| 1 |
| 2 |
| 9 |
| 2 |
∴
| a |
| b+c |
| b |
| c+a |
| c |
| a+b |
| 3 |
| 2 |
∴
| a |
| b+c |
| b |
| c+a |
| c |
| a+b |
| 3 |
| 2 |
点评:柯西不等式的特点:一边是平方和的积,而另一边为积的和的平方,因此,当欲证不等式的一边视为“积和结构”或“平方和结构”,再结合不等式另一边的结构特点去尝试构造.

练习册系列答案
相关题目
在复平面内,若复数z=(x2-9)+(x-3)i为纯虚数,则实数x值为( )
| A、-3 | B、0 | C、3 | D、-3或3 |
在(
+
)n的二项展开式中,第三项的系数与第二项的系数的差为20,则展开式中含
的项的系数为( )
| x |
| 1 |
| x2 |
| 1 |
| x |
| A、8 | B、28 | C、56 | D、70 |
y=2cosx的图象经过怎样的变换能变成函数y=2cos(2x+
)的图象( )
| π |
| 3 |
A、向左平移
| ||||
B、向左平移
| ||||
C、将图象上各点的横坐标缩短到原来的
| ||||
D、将图象上各点的横坐标伸长到原来的2倍,纵坐标不变,再向左平移
|
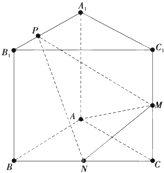 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N分别是CC1,BC的中点,点P在线段A1B1上,且
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N分别是CC1,BC的中点,点P在线段A1B1上,且