题目内容
在x(1+x)6的展开式中,含x3项的系数为( )
| A、30 | B、20 | C、15 | D、10 |
考点:二项式系数的性质
专题:二项式定理
分析:利用二项展开式的通项公式求出(1+x)6的第r+1项,令x的指数为2求出展开式中x2的系数.然后求解即可.
解答:
解:(1+x)6展开式中通项Tr+1=C6rxr,
令r=2可得,T3=C62x2=15x2,
∴(1+x)6展开式中x2项的系数为15,
在x(1+x)6的展开式中,含x3项的系数为:15.
故选:C.
令r=2可得,T3=C62x2=15x2,
∴(1+x)6展开式中x2项的系数为15,
在x(1+x)6的展开式中,含x3项的系数为:15.
故选:C.
点评:本题考查二项展开式的通项的简单直接应用.牢记公式是基础,计算准确是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设向量
,
满足|
+
|=
,|
-
|=
,则
•
=( )
| a |
| b |
| a |
| b |
| 10 |
| a |
| b |
| 6 |
| a |
| b |
| A、1 | B、2 | C、3 | D、5 |
如图所示,程序框图(算法流程图)的输出结果是( )


| A、22 | B、16 | C、15 | D、11 |
设函数f(x)=x2sinx,则函数f(x)的图象可能为( )
A、 |
B、 |
C、 |
D、 |
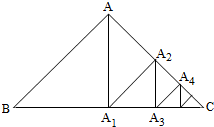 如图,在等腰直角三角形ABC中,斜边BC=2
如图,在等腰直角三角形ABC中,斜边BC=2
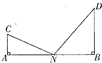 如图,C、D是两个小区所在地,C、D到一条公路AB的垂直距离分别为CA=1km,DB=2km,A、B间的距离为3km,某公交公司要在A、B之间的某点N处建造一个公交站点,使得N对C、D两个小区的视角∠CND最大,则N处与A处的距离为
如图,C、D是两个小区所在地,C、D到一条公路AB的垂直距离分别为CA=1km,DB=2km,A、B间的距离为3km,某公交公司要在A、B之间的某点N处建造一个公交站点,使得N对C、D两个小区的视角∠CND最大,则N处与A处的距离为