题目内容
若a0+a1(2x-1)+a2(2x-1)2+a3(2x-1)3+a4(2x-1)4=x4,则a2= .
考点:二项式系数的性质
专题:二项式定理
分析:把x4=[
(2x-1)+
]4按照二项式定理展开,再根据x4=a4(2x-1)4+a3(2x-1)3+a2(2x-1)2+a1(2x-1)+a0 ,比较系数求得a2的值.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:∵x4=[
(2x-1)+
]4=C40 (2x-1)4•(
)4+C41(2x-1)3•(
)4+C42(2x-1)2•(
)4+C43(2x-1)(
)4+C44(
)4,
又由题意得,x4=[
(2x-1)+
]4 =
•[(2x-1)+1]4=a4(2x-1)4+a3(2x-1)3+a2(2x-1)2+a1(2x-1)+a0 ,
∴a2=
•
=
,
故答案为:
.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又由题意得,x4=[
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 24 |
∴a2=
| 1 |
| 24 |
| C | 2 4 |
| 3 |
| 8 |
故答案为:
| 3 |
| 8 |
点评:本题考查二项式定理系数的性质,通项公式的应用,考查转化思想的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
将函数y=sin2x+
cos2x(x∈R)的图象向右平移m(m>0)个单位长度后,所得到的图象关于原点对称,则m的最小值为( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
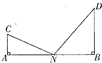 如图,C、D是两个小区所在地,C、D到一条公路AB的垂直距离分别为CA=1km,DB=2km,A、B间的距离为3km,某公交公司要在A、B之间的某点N处建造一个公交站点,使得N对C、D两个小区的视角∠CND最大,则N处与A处的距离为
如图,C、D是两个小区所在地,C、D到一条公路AB的垂直距离分别为CA=1km,DB=2km,A、B间的距离为3km,某公交公司要在A、B之间的某点N处建造一个公交站点,使得N对C、D两个小区的视角∠CND最大,则N处与A处的距离为