题目内容
已知函数f(x)=loga|x+1|,当x∈(0,1)时,恒有f(x)<0,则函数g(x)=loga (
)的递减区间是 .
| -3 |
| 2x2+ax |
考点:函数单调性的判断与证明
专题:函数的性质及应用,导数的综合应用
分析:先根据已知条件求出a的取值范围,求出函数g(x)的定义域,求g′(x),解不等式g′(x)<0即可得出g(x)的单调递减区间.
解答:
解:x∈(0,1)时,x+1∈(1,2),logax+1<0,∴0<a<1;
解
>0,得-
<x<0,即g(x)的定义域为(-
,0);
解g′(x)=
<0得-
<x<0,或x<-
(舍去);
∴g(x)的递减区间是:(-
,0).
故答案为:(-
,0).
解
| -3 |
| 2x2+ax |
| a |
| 2 |
| a |
| 2 |
解g′(x)=
| (2x2+ax)(4x+a) |
| -3lna |
| a |
| 4 |
| a |
| 2 |
∴g(x)的递减区间是:(-
| a |
| 4 |
故答案为:(-
| a |
| 4 |
点评:考查对数函数单调性及图象,解一元二次不等式,一元三次不等式,函数导数符号和函数单调区间的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
两个等差数列{an}和{bn},前n项和分别为Sn,Tn,且
=
,则
=( )
| Sn |
| Tn |
| 9n+36 |
| n+4 |
| a2+a20 |
| b7+b15 |
| A、9 | ||
B、
| ||
C、
| ||
D、
|
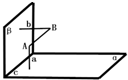 如图,已知直线a⊥平面α,b⊥β,且AB⊥a,AB⊥b,平面α∩β=直线c,求证:直线AB∥c.
如图,已知直线a⊥平面α,b⊥β,且AB⊥a,AB⊥b,平面α∩β=直线c,求证:直线AB∥c.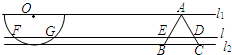 如图,半径为1的半圆O与等边△ABC夹在两平行线l1、l2之间.l∥l1,l与半圆相交于F、G两点,与三角形ABC两边相交于E、D两点,设弧
如图,半径为1的半圆O与等边△ABC夹在两平行线l1、l2之间.l∥l1,l与半圆相交于F、G两点,与三角形ABC两边相交于E、D两点,设弧