题目内容
已知函数f(x)=loga[(
-2)x+1]的区间[1,2]上恒为正值,求实数a的取值范围.
| 1 |
| a |
考点:函数恒成立问题
专题:函数的性质及应用
分析:应该分a>1和0<a<1两种情况讨论,确定真数的范围,使得该对数恒为正.
解答:
解:①当a>1时,要使f(x)恒为正,只需真数(
-2)x+1当x∈[1,2]时恒大于1,
令y=(
-2)x+1,该函数在[1,2]上是单调函数,因此只需
,无解;
②当0<a<1时,要使f(x)恒为正,只需真数y=(
-2)x+1当x∈[1,2]时,在区间(0,1)内取值,
而y=(
-2)x+1在[1,2]上是单调函数,所以只需
,解得
<a<
.
综上,a的范围是
<a<
.
| 1 |
| a |
令y=(
| 1 |
| a |
|
②当0<a<1时,要使f(x)恒为正,只需真数y=(
| 1 |
| a |
而y=(
| 1 |
| a |
|
| 1 |
| 2 |
| 2 |
| 3 |
综上,a的范围是
| 1 |
| 2 |
| 2 |
| 3 |
点评:本题一方面考查了对数函数的性质,要结合对数函数的图象来解决问题;另一方面要注意分类讨论.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
两个等差数列{an}和{bn},前n项和分别为Sn,Tn,且
=
,则
=( )
| Sn |
| Tn |
| 9n+36 |
| n+4 |
| a2+a20 |
| b7+b15 |
| A、9 | ||
B、
| ||
C、
| ||
D、
|
代数式a-5的值为正数时,a应满足条件( )
| A、a<5 | B、a<4 |
| C、a>5 | D、a<0 |
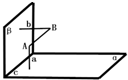 如图,已知直线a⊥平面α,b⊥β,且AB⊥a,AB⊥b,平面α∩β=直线c,求证:直线AB∥c.
如图,已知直线a⊥平面α,b⊥β,且AB⊥a,AB⊥b,平面α∩β=直线c,求证:直线AB∥c.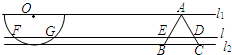 如图,半径为1的半圆O与等边△ABC夹在两平行线l1、l2之间.l∥l1,l与半圆相交于F、G两点,与三角形ABC两边相交于E、D两点,设弧
如图,半径为1的半圆O与等边△ABC夹在两平行线l1、l2之间.l∥l1,l与半圆相交于F、G两点,与三角形ABC两边相交于E、D两点,设弧