题目内容
某市2013年发放汽车牌照12万张，其中燃油型汽车牌照10万张，电动型汽车2万张．为了节能减排和控制总量，从2013年开始，每年电动型汽车牌照按50%增长，而燃油型汽车牌照每一年比上一年减少0.5万张，同时规定一旦某年发放的牌照超过15万张，以后每一年发放的电动车的牌照的数量维持在这一年的水平不变．
（1）记2013年为第一年，每年发放的燃油型汽车牌照数构成数列{an}，每年发放的电动型汽车牌照数为构成数列{bn}，完成下列表格，并写出这两个数列的通项公式；
（2）从2013年算起，求二十年发放的汽车牌照总量．
（1）记2013年为第一年，每年发放的燃油型汽车牌照数构成数列{an}，每年发放的电动型汽车牌照数为构成数列{bn}，完成下列表格，并写出这两个数列的通项公式；
| a1=10 | a2=9.5 | a3= |
a4= |
… |
| b1=2 | b2= |
b3= |
b4= |
… |
考点：数列的应用,数列的求和
专题：计算题,点列、递归数列与数学归纳法
分析：（1）利用从2013年开始，每年电动型汽车牌照按50%增长，而燃油型汽车牌照每一年比上一年减少0.5万张，同时规定一旦某年发放的牌照超过15万张，以后每一年发放的电动车的牌照的数量维持在这一年的水平不变，可填写表格，并写出这两个数列的通项公式；
（2）利用等差数列与等比数列的求和公式，可求从2013年算起，求二十年发放的汽车牌照总量．
（2）利用等差数列与等比数列的求和公式，可求从2013年算起，求二十年发放的汽车牌照总量．
解答：
解：（1）
…（2分）
当1≤n≤20且n∈N*，an=10+（n-1）×（-0.5）=-0.5n+10.5；
当n≥21且n∈N*，an=0．
∴an=
…（5分）
而a4+b4=15.25＞15
∴bn=
，…（8分）
（2）a1+a2+…+a20=10×20+
•(-
)=105…（10分）
b1+b2+b3+b4+b5+…+b20=
+6.75×16=124.25…（13分）
∴从2013年算起，二十年发放的汽车牌照总量为229.25万张．…（14分）
| a1=10 | a2=9.5 | a3=9 | a4=8.5 | … |
| b1=2 | b2=3 | b3=4.5 | b4=6.75 | … |
当1≤n≤20且n∈N*，an=10+（n-1）×（-0.5）=-0.5n+10.5；
当n≥21且n∈N*，an=0．
∴an=
|
而a4+b4=15.25＞15
∴bn=
|
（2）a1+a2+…+a20=10×20+
| 20×1 |
| 2 |
| 1 |
| 2 |
b1+b2+b3+b4+b5+…+b20=
2[1-(
| ||
1-
|
∴从2013年算起，二十年发放的汽车牌照总量为229.25万张．…（14分）
点评：本题考查数列的应用，考查利用数学知识解决实际问题，考查数列的求和，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
设y=ln（2x+3），则y′=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
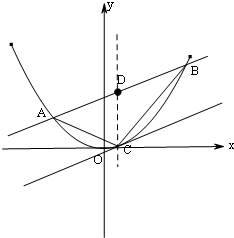如图，直线l：y=kx+b与抛物线x2=2py（常数p＞0）相交于不同的两点A（x1，y1）、B（x2，y2），且|x2-x1|=h（h为定值），线段AB的中点为D，与直线l：y=kx+b平行的切线的切点为C（不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线，这个公共点为切点）．
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”，每班50人，吴老师采用A、B两种不同的教学方式分别在甲、乙两个班进行教学实验．为了解教学效果，期末考试后，分别从两个班级中各随机抽取20名学生的成绩进行统计，作出的茎叶图如图所示．记成绩不低于90分者为“成绩优秀”．
如图，在三棱柱ABC-A1B1C1中，已知AB⊥侧面BB1C1C，AB=BC=1，BB1=2，∠BCC1=