题目内容
5.设数列{an}的前n项和为Sn,且2an+Sn=-1.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若实数λ满足$\frac{1}{{{{({S_n}+1)}^2}}}-\frac{1}{a_n^2}≥\frac{λ}{{{a_n}{a_{n+1}}}}$,求λ的最大值.
分析 (Ⅰ)推导出2an-2an-10+an=0,从而$\frac{{a}_{n}}{{a}_{n-1}}=\frac{2}{3}$,再由2a1+S1=-1,得到数列{an}是以-$\frac{1}{3}$为首项,$\frac{2}{3}$为公比的等比数列,由此能求出数列{an}的通项公式.
(Ⅱ)求出Sn=($\frac{2}{3}$)n-1,从而不等式$\frac{1}{(\frac{2}{3})^{2n}}$-$\frac{9}{(\frac{2}{3})^{2n-2}}$≥$\frac{9λ}{(\frac{2}{3})^{2n-1}}$,由此能求出λ的最大值.
解答 解:(Ⅰ)∵数列{an}的前n项和为Sn,且2an+Sn=-1.
∴n≥2时,2an-1+Sn-1=-1,
两式相减,得2an-2an-1+an=0,即$\frac{{a}_{n}}{{a}_{n-1}}=\frac{2}{3}$,
又2a1+S1=-1,∴${a}_{1}=-\frac{1}{3}$,
∴数列{an}是以-$\frac{1}{3}$为首项,$\frac{2}{3}$为公比的等比数列,
∴数列{an}的通项公式${a}_{n}=-\frac{1}{3}•(\frac{2}{3})^{n-1}$.
(Ⅱ)由(Ⅰ)知,Sn=$\frac{-\frac{1}{3}[1-(\frac{2}{3})^{n}]}{1-\frac{2}{3}}$=($\frac{2}{3}$)n-1,
∴不等式$\frac{1}{({S}_{n}+1)^{2}}$-$\frac{1}{{{a}_{n}}^{2}}$≥$\frac{λ}{{a}_{n}{a}_{n+1}}$,即$\frac{1}{(\frac{2}{3})^{2n}}$-$\frac{9}{(\frac{2}{3})^{2n-2}}$≥$\frac{9λ}{(\frac{2}{3})^{2n-1}}$,
两边同时乘以($\frac{2}{3}$)2n,得1-$9×(\frac{2}{3})^{2}≥9λ×\frac{2}{3}$,
解得$λ≤-\frac{1}{2}$,∴λ的最大值为-$\frac{1}{2}$.
点评 本题考查数列有通项公式的求法,考查实数的最大值的求法,涉及到等比数列、不等式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案| A. | -1 | B. | 2 | C. | $-\frac{{\sqrt{5}}}{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
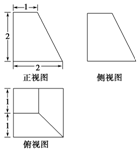
| A. | 12 | B. | $\frac{14}{3}$ | C. | $6+3\sqrt{5}$ | D. | $11+3\sqrt{5}$ |
| A. | a,b都为偶数 | B. | a,b不为偶数 | ||
| C. | a,b都不为偶数 | D. | a,b中有一个不为偶数 |
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
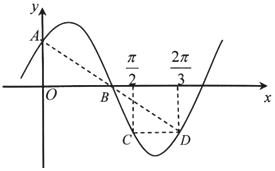 如图,已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π),点A,B分别是f(x)的图象与y轴、x轴的交点,C,D分别是f(x)的图象上横坐标为$\frac{π}{2}$、$\frac{2π}{3}$的两点,CD∥x轴,A,B,D共线.
如图,已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π),点A,B分别是f(x)的图象与y轴、x轴的交点,C,D分别是f(x)的图象上横坐标为$\frac{π}{2}$、$\frac{2π}{3}$的两点,CD∥x轴,A,B,D共线.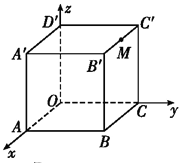 如图,棱长为2的正方体OABC-D′A′B′C′中,点M在B′C′上,且M为B′C′的中点,若以O为坐标原点,建立空间直角坐标系,则点M的坐标为(1,2,2).
如图,棱长为2的正方体OABC-D′A′B′C′中,点M在B′C′上,且M为B′C′的中点,若以O为坐标原点,建立空间直角坐标系,则点M的坐标为(1,2,2).