题目内容
19.已知函数f(x)=aex-1-1(x∈R),若方程f(x)+|x-a|=0有且仅有两个不相等的实根,则实数a的取值范围为[0,1)∪{-1}.分析 根据函数和方程之间的关系讲方程转化为f(x)=-|x-a|,利用数形结合分别作出函数f(x)与g(x)=-|x-a|的图象,利用数形结合进行求解即可.
解答 解:由f(x)+|x-a|=0得f(x)=-|x-a|,
设g(x)=-|x-a|,
①若a=0,则f(x)=-1,g(x)=-|x|,作出f(x)和g(x)的图象如图:此时两个函数有两个交点,满足条件,
②若a>0,则函数g(x)的零点为(a,0),
由f(x)=0得aex-1-1=0,即ex-1=$\frac{1}{a}$,
则x-1=ln$\frac{1}{a}$=-lna,
则x=1-lna,
即f(x)的零点为(1-lna,0),
若两个函数有两个零点,
则1-lna>a,即1-lna-a>0,
设h(a)=1-lna-a,则函数在(0,+∞)上为减函数,
∵h(1)=1-ln1-1=0,
∴由h(a)>0得h(a)>h(1),得a<1.
即此时0<a<1,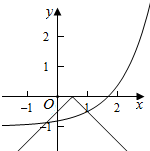
③若a<0,当x>a时,g(x)=-|x-a|=-x+a,
当g(x)与f(x)相切时,满足有两个交点,
此时f′(x)=aex-1,设切点为(m,n),
则切线斜率k=aem-1,n=aem-1-1,即切点坐标为(m,aem-1-1),
则切线方程为y-(aem-1-1)=aem-1(x-m),
即y=aem-1(x-m)+(aem-1-1)=aem-1•x-maem-1+aem-1-1,
∵g(x)=-x+a
∴aem-1=-1,-maem-1+aem-1-1=a,
得m-1-1=a,即m=a+2,
则aea+2-1=-1,即aea+1=-1,
得a=-1,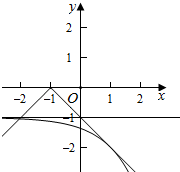
综上所述,0≤a<1或a=-1
故答案为:[0,1)∪{-1}
点评 本题主要考查根的个数的判断,根据函数与方程的关系,转化为两个函数的交点问题,利用分类讨论的数学思想进行求解即可,综合性较强,难度较大.

| A. | y=x2sin(x+$\frac{π}{3}$) | B. | y=x2cos$\frac{x}{3}$ | C. | y=tan(x-$\frac{π}{3}$) | D. | y=x3tanx2 |
| A. | $f(ln\frac{3}{2})sin(ln\frac{3}{2})$一定小于$0.6f(ln\frac{5}{2})sin(ln\frac{5}{2})$ | |
| B. | $f(ln\frac{3}{2})sin(ln\frac{3}{2})$一定大于$0.6f(ln\frac{5}{2})sin(ln\frac{5}{2})$ | |
| C. | $f(ln\frac{3}{2})sin(ln\frac{3}{2})$可能大于$0.6f(ln\frac{5}{2})sin(ln\frac{5}{2})$ | |
| D. | $f(ln\frac{3}{2})sin(ln\frac{3}{2})$可能等于$0.6f(ln\frac{5}{2})sin(ln\frac{5}{2})$ |
| A. | 61个 | B. | 63个 | C. | 65个 | D. | 67个 |
| A. | 60° | B. | 45° | C. | 90° | D. | 30° |