题目内容
9.已知正方体ABCD-A1B1C1D1中,E,F分别是A1D1,D1C1的中点,则异面直线EF与AB1所成角为( )| A. | 60° | B. | 45° | C. | 90° | D. | 30° |
分析 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出异面直线EF与AB1所成角.
解答 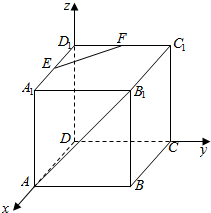 解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设正方体ABCD-A1B1C1D1中棱长为2,
则E(1,0,2),F(0,1,2),A(2,0,0),B1(2,2,2),
$\overrightarrow{EF}$=(-1,1,0),$\overrightarrow{A{B}_{1}}$=(0,2,2),
设异面直线EF与AB1所成角为θ,
cosθ=$\frac{|\overrightarrow{EF}•\overrightarrow{A{B}_{1}}|}{|\overrightarrow{EF}|•|\overrightarrow{A{B}_{1}}|}$=$\frac{|2|}{\sqrt{2}•\sqrt{8}}$=$\frac{1}{2}$,
∴θ=60°.
故选:A.
点评 本题考查异面直线所成角的大小的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
20.甲、乙两名运动员进行射击训练,已知他们击中目标的环数均稳定在7,8,9,10环,且每次射击成绩互不影响,射击环数的频率分布表如表:
甲运动员
乙运动员
如果将频率视为概率,回答下面的问题:
(Ⅰ)写出x,y,z的值;
(Ⅱ)求甲运动员在三次射击中,至少有一次命中9环(含9环)以上的概率;
(Ⅲ)若甲运动员射击2次,乙运动员射击1次,用ξ表示这三次中射击击中9环的次数,求ξ的概率分布列及Eξ.
甲运动员
| 射击环数 | 频数 | 频率 |
| 7 | 10 | |
| 8 | 10 | |
| 9 | x | |
| 10 | 30 | y |
| 合计 | 100 | 1 |
| 射击环数 | 频数 | 频率 |
| 7 | 6 | |
| 8 | 10 | |
| 9 | z | 0.4 |
| 10 | ||
| 合计 | 80 |
(Ⅰ)写出x,y,z的值;
(Ⅱ)求甲运动员在三次射击中,至少有一次命中9环(含9环)以上的概率;
(Ⅲ)若甲运动员射击2次,乙运动员射击1次,用ξ表示这三次中射击击中9环的次数,求ξ的概率分布列及Eξ.
4.(x2+3y-y2)7展开式中,x12y2项系数为( )
| A. | 7 | B. | -7 | C. | 42 | D. | -42 |
14.在空间直角坐标系中,已知三点A(1,0,0),B(1,1,1),C(0,1,1),则三角形ABC 是( )
| A. | 直角三角形 | B. | 等腰三角形 | C. | 等腰直角三角形 | D. | 等边三角形 |
1.将函数y=sinx的图象上所有点的横坐标缩小到原来的$\frac{1}{2}$(纵坐标不变),再将所得到的图象上所有点向左平移$\frac{π}{6}$个单位,所得函数图象的解析式为( )
| A. | y=sin(2x-$\frac{π}{3}$) | B. | y=sin(2x+$\frac{π}{3}$) | C. | y=sin($\frac{1}{2}$x+$\frac{π}{3}$) | D. | y=sin($\frac{1}{2}$x+$\frac{π}{6}$) |
18.函数y=sinx+tanx,x∈[-$\frac{π}{4}$,$\frac{π}{4}$]的值域是( )
| A. | [-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$] | B. | [-2,2] | C. | [-$\frac{\sqrt{2}}{2}$-1,$\frac{\sqrt{2}}{2}$] | D. | [-$\frac{\sqrt{2}}{2}$-1,$\frac{\sqrt{2}}{2}$+1] |