题目内容
4.设x0为函数f(x)=sinπx的零点,且满足|x0|+f(x0+$\frac{1}{2}$)<33,则这样的零点有( )| A. | 61个 | B. | 63个 | C. | 65个 | D. | 67个 |
分析 根据函数零点的定义,先求出x0的值,进行求出f(x0+$\frac{1}{2}$)的值,然后解不等式即可.
解答 解:∵x0为函数f(x)=sinπx的零点,
∴sinπx0=0,即πx0=kπ,k∈Z,
则x0=k,则f(x0+$\frac{1}{2}$)=sin(x0+$\frac{1}{2}$)π=sin(πx0+$\frac{π}{2}$)=cosπx0,
若k是偶数,则f(x0+$\frac{1}{2}$)=1,
若k是奇数,则f(x0+$\frac{1}{2}$)=-1,
当k是偶数时,则由|x0|+f(x0+$\frac{1}{2}$)<33得|x0|<-f(x0+$\frac{1}{2}$)+33,
即|k|<-1+33=32,
则k=-30,-28,…28,30,共31个,
当k是奇数时,则由|x0|+f(x0+$\frac{1}{2}$)<33得|x0|<-f(x0+$\frac{1}{2}$)+33,
即|k|<1+33=34,
则k=-33,-31,…31,33,共34个,
故共有31+34=65个,
故选:C.
点评 本题主要考查函数与方程的应用,根据三角函数的性质,求出函数的零点,利用分类讨论思想是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.等比数列{an}的前n项和为Sn,若公比q=4,S3=21,则( )
| A. | 4an=1-3Sn | B. | 4Sn=3an-1 | C. | 4Sn=3an+1 | D. | 4an=3Sn+1 |
16.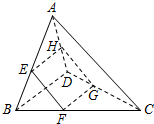 如图,在四面体A-BCD中,AC与BD互相垂直,且长度分别为2和3,平行于这两条棱的平面与边AB、BC、CD、DA分别相交于点E、F、G、H,记四边形EFGH的面积为y,设$\frac{BE}{AB}$=x,则( )
如图,在四面体A-BCD中,AC与BD互相垂直,且长度分别为2和3,平行于这两条棱的平面与边AB、BC、CD、DA分别相交于点E、F、G、H,记四边形EFGH的面积为y,设$\frac{BE}{AB}$=x,则( )
 如图,在四面体A-BCD中,AC与BD互相垂直,且长度分别为2和3,平行于这两条棱的平面与边AB、BC、CD、DA分别相交于点E、F、G、H,记四边形EFGH的面积为y,设$\frac{BE}{AB}$=x,则( )
如图,在四面体A-BCD中,AC与BD互相垂直,且长度分别为2和3,平行于这两条棱的平面与边AB、BC、CD、DA分别相交于点E、F、G、H,记四边形EFGH的面积为y,设$\frac{BE}{AB}$=x,则( )| A. | 函数f(x)的值域为(0,1] | B. | 函数y=f(x)满足f(x)=f(2-x) | ||
| C. | 函数y=f(x)的最大值为2 | D. | 函数y=f(x)在(0,$\frac{1}{2}$)上单调递增 |
14.在空间直角坐标系中,已知三点A(1,0,0),B(1,1,1),C(0,1,1),则三角形ABC 是( )
| A. | 直角三角形 | B. | 等腰三角形 | C. | 等腰直角三角形 | D. | 等边三角形 |
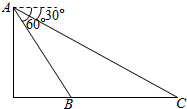 如图,从高为$200\sqrt{3}$米的气球(A)上测量铁桥(BC)的长,如果测得桥头B的俯角是60°,桥头C的俯角是30°,则桥BC长为400米.
如图,从高为$200\sqrt{3}$米的气球(A)上测量铁桥(BC)的长,如果测得桥头B的俯角是60°,桥头C的俯角是30°,则桥BC长为400米.